Сторінка
1

Векторна функція скалярного аргументу. Похідна, її геометричний і механічний зміст. Кривизна кривої

План

• Диференціал дуги
• Кривизна плоскої кривої
• Векторна функція скалярного аргументу
• Кривизна плоскої кривої
• Кривизна просторової кривої
• Кручення просторової лінії
• Формули Серре-Френе

1. Диференціал кривої

Поняття довжини кривої буде розглянуто в розділі інтегрального числення. Криві, для яких можна установити поняття довжини, називають в математичному аналізі спрямними.

Умова спрямності кривої для плоскої кривої, заданої параметричними рівняннями , полягає в такому: на спрямному відрізку кривої функції і мусять мати неперервні похідні за параметром : . Аналогічною є умова спрямності просторової кривої, заданої рівняннями ; вона полягає в неперервності похідних .

Для всякої спрямної кривої як просторової, так і плоскої, наслідком її спрямності є така геометрична властивість: границя відношення нескінченно малої дуги кривої до стягуючої її хорди дорівнює одиниці за умови, що хорда стикується в точку.

Якщо довжину малої дуги кривої позначити через , а довжину відповідної хорди – через (рис. 7.4), то

(7.4)

Виходячи саме з цієї властивості, знайдемо вирази для диференціала дуги як плоскої, так і просторової кривої.

На плоскій спрямній кривій, рівняння якої ,

візьмемо дві сусідні точки. та , що

відповідають значенням параметра та (рис. 7.2).

Довжина хорди знаходиться за формулою

(7.5)

Похідна від довжини дуги кривої за параметром :

.

Замінимо його виразом за формулою (7.5):

.

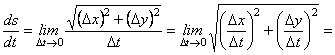
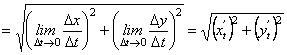Отже,

. (7.6)

Звідси

. (7.7)

Якщо крива задана рівнянням , то можна прийняти за параметр кривої:.

Диференціал дуги

Якщо крива задана рівнянням в полярних координатах , то за параметр кривої можна прийняти полярний кут .

Диференціюємо по рівності

Маємо

.

Звідси

,

тому

. (7.9)

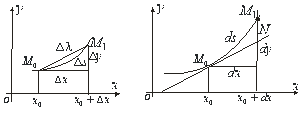
Рис.7.4 Рис.7.5

Приклади.

1. Знайти диференціал дуги циклоїди

.

Р о з в ’ я з о к. .

.

2. Знайти диференціал дуги кардіоїди .

Р о з в ’ я з о к. ,

.

Диференціал дуги просторової кривої, заданої параметричними рівняннями , можна знайти аналогічно.

Відміна від попереднього полягає лише в тому, що довжина хорди, яка з’єднує точки просторової кривої і визначається за формулою