Сторінка
6

Векторна функція скалярного аргументу. Похідна, її геометричний і механічний зміст. Кривизна кривої

Знайдемо вектор . Для цього диференціюємо рівність :

,

або

Формули

(7.34)

називаються формулами Серре-Френе, це основні формули геометрії просторових кривих.

Виведемо формули для кривизни та кручення просторової кривої, яка задана векторним рівнянням .

Перша із формул Серре-Френе дає

, (7.35)

оскільки . Домножимо другу із формул Серре-Френе скалярно на вектор :

.

Але

,

,

тому

.

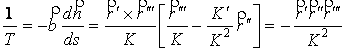(7.36)

В координатній формі ці формули мають такий вигляд

(7.37)

Якщо вектор заданий як функція довільного параметру ( а не довжини дуги ), то формули (7.35) і (7.36) набувають вигляду:

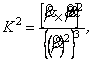
(7.38)

Вектори, колінеарні одиничним векторам та будемо позначати та . Щоб написати рівняння дотичної, головної нормалі, бінормалі та будь-якої із площин супроводжуючого тригранника, достатньо лише в канонічних рівняннях прямої

(7.39)

і в рівнянні площини, яка проходить через дану точку

, (7.40)

взяти за координати вибраної на просторовій кривій точки, а за та або відповідно та - координати того із векторів або , який визначається напрямком шуканої прямої або нормалі до шуканої площини: або для дотичної та нормальної площини, і - для головної нормалі та спрямної площини, або - для бінормалі та співдотичної площини.

Нехай просторова крива задана векторним рівнянням , або, що те саме, рівнянням

.

За вектор , який має напрямок дотичної до кривої, можна взяти вектор .

Отже,

. (7.41)

Для відшукання векторів , що мають напрямок головної нормалі та бінормалі, знайдемо спочатку розклад вектора за векторами .

Оскільки

.

то

. (7.42)

Перемножимо вектори та :

(7.43)

Звідси

(7.44)

Тоді за вектор через його перпендикулярність до векторів та можна взяти векторний добуток цих двох векторів:

(7.45)

Цим самим ми дістали можливість в будь-якій точці просторової кривої визначити всі елементи його супровідного тригранника.