Сторінка
1
1. Загальна теорія
Якщо ліва частина диференціального рівняння
![]()
є повним диференціалом деякої функції ![]() , тобто
, тобто
![]() ,
,
і, таким чином, рівняння приймає вигляд ![]() то рівняння називається рівнянням в повних диференціалах. Звідси вираз
то рівняння називається рівнянням в повних диференціалах. Звідси вираз
![]()
є загальним інтегралом диференціального рівняння.
Критерієм того, що рівняння є рівнянням в повних диференціалах, тобто необхідною та достатньою умовою, є виконання рівності
![]()
Нехай маємо рівняння в повних диференціалах. Тоді
![]()
Звідси ![]() де
де ![]() - невідома функція. Для її визначення продиференціюємо співвідношення по
- невідома функція. Для її визначення продиференціюємо співвідношення по ![]() і прирівняємо
і прирівняємо ![]()
![]()
Звідси
![]() .
.
Остаточно, загальний інтеграл має вигляд
![]()
Як відомо з математичного аналізу, якщо відомий повний диференціал
![]() ,
,
то![]() можна визначити, взявши криволінійний інтеграл по довільному контуру, що з’єднує фіксовану точку
можна визначити, взявши криволінійний інтеграл по довільному контуру, що з’єднує фіксовану точку![]() і точку із змінними координатами
і точку із змінними координатами ![]() . Більш зручно брати криву, що складається із двох відрізків прямих. В цьому випадку криволінійний інтеграл розпадається на два простих інтеграла
. Більш зручно брати криву, що складається із двох відрізків прямих. В цьому випадку криволінійний інтеграл розпадається на два простих інтеграла
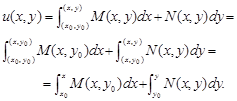
В цьому випадку одразу одержуємо розв’язок задачі Коші.
![]() .
.
2. Множник, що Інтегрує
В деяких випадках рівняння
![]()
не є рівнянням в повних диференціалах, але існує функція ![]() така, що рівняння
така, що рівняння
![]()
вже буде рівнянням в повних диференціалах. Необхідною та достатньою умовою цього є рівність
![]() ,
,
або
![]() .
.
Таким чином замість звичайного диференціального рівняння відносно функції ![]() одержимо диференціальне рівняння в частинних похідних відносно функції
одержимо диференціальне рівняння в частинних похідних відносно функції ![]() . Задача інтегрування його значно спрощується, якщо відомо в якому вигляді шукати функцію
. Задача інтегрування його значно спрощується, якщо відомо в якому вигляді шукати функцію ![]() , наприклад
, наприклад ![]() де
де ![]() - відома функція. В цьому випадку одержуємо
- відома функція. В цьому випадку одержуємо
![]()
Після підстановки в рівняння маємо
![]() ,
,
або
![]() .
.
Розділимо змінні
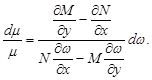
Проінтегрувавши і поклавши сталу інтегрування одиницею, одержимо:
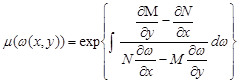 .
.
Розглянемо частинні випадки.
1) Нехай ![]() . Тоді
. Тоді ![]()
І формула має вигляд
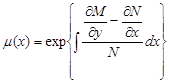 .
.
2) Нехай ![]() . Тоді
. Тоді ![]()
І формула має вигляд
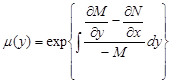
3) Нехай ![]() .Тоді
.Тоді
![]()
І формула має вигляд
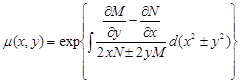 .
.
4) Нехай ![]() . Тоді
. Тоді ![]()
І формула має вигляд
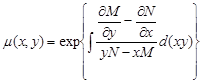 .
.
Інші реферати на тему «Математика»:
Основні властивості означеного інтеграла. Формула Ньютона- Лейбніца
Особливості вивчення математики в профільних класах у сучасних умовах
Синтез систем з оптимізацією модальних регуляторів
Задачі геометричного і фізичного змісту, що приводить до поняття подвійного інтеграла
Інтегрування ірраціональних виразів
