Сторінка
1

Диференціальні рівняння першого порядку, не розв’язані відносно похідної

Диференціальне рівняння першого порядку, не розв’язане відносно похідної, має такий вигляд

Частинні випадки рівнянь, що інтегруються в квадратурах

Розглянемо ряд диференціальних рівнянь, що інтегруються в квадратурах.

1) Рівняння вигляду . Нехай алгебраїчне рівняннямає по крайній мірі один дійсний корінь . Тоді, інтегруючи , одержимо . Звідси і вираз містить всі розв’язки вихідного диференціального рівняння.

2) Рівняння вигляду . Нехай це рівняння можна записати у параметричному вигляді

Використовуючи співвідношення , одержимо . Проінтегрувавши, запишемо

.

І загальний розв’язок в параметричній формі має вигляд

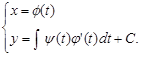
3) Рівняння вигляду . Нехай це рівняння можна записати у параметричному вигляді

Використовуючи співвідношення , отримаємо і . Проінтегрувавши, запишемо

.

І загальний розв’язок в параметричній формі має вигляд

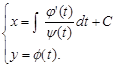
4) Рівняння Лагранжа

.

Введемо параметрі отримаємо

Продиференціювавши, запишемо

Замінивши одержимо

Звідси

І отримали лінійне неоднорідне диференціальне рівняння

Його розв’язок

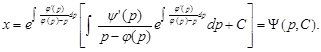
І остаточний розв’язок рівняння Лагранжа в параметричній формі запишеться у вигляді

5) Рівняння Клеро.

Частинним випадком рівняння Лагранжа, що відповідає є рівняння Клеро

Поклавши , отримаємо . Продиференцюємо Оскільки , то

Скоротивши, одержимо Можливі два випадки.

1. і розв’язок має вигляд

2.і розв’язок має вигляд

.

Загальним розв’язком рівняння Клеро буде сім’я прямих . Цю сім’ю огинає особа крива , .

6) Параметризація загального вигляду. Нехай диференціальне рівняння вдалося записати у вигляді системи рівнянь з двома параметрами

.

Використовуючи співвідношення , одержимо

.

Перегрупувавши члени, одержимо

.

Звідси

.

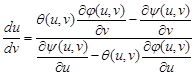Або отримали рівняння вигляду

.

Параметризація загального вигляду не дає інтеграл диференціального рівняння. Вона дозволяє звести диференціальне рівняння, не розв’язане відносно похідної, до диференціального рівняння, розв’язаного відносно похідної.

7) Нехай рівняння можна розв’язати відносно і воно має -коренів, тобто його можна записати у вигляді .

Розв’язавши кожне з рівнянь , отримаємо загальних розв’язків (або інтервалів) (або ). І загальний розв’язок вихідного рівняння, не розв’язаного відносно похідної має вигляд