Сторінка
1

Системи лінійних диференціальних рівнянь. Загальні положення

Система диференціальних рівнянь, що записана у вигляді

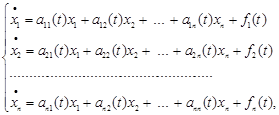
називається лінійною неоднорідною системою диференціальних рівнянь. Система

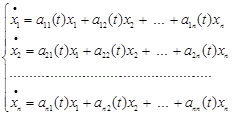
називається лінійною однорідною системою диференціальних рівнянь. Якщо ввести векторні позначення

,, ,

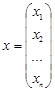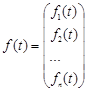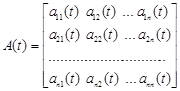то лінійну неоднорідну систему можна переписати у вигляді

а лінійну однорідну систему у вигляді

.

Якщо функції неперервні в околі точки , товиконані умови теореми існування та єдиності розв’язку задачі Коші, і існує єдиний розв’язок

системи рівнянь, що задовольняє початковим даним

1. Властивості розв’язків лінійних однорідних систем

Властивість 1. Якщо вектор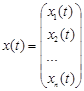є розв’язком лінійної однорідної системи, то і 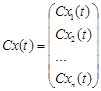, де - стала скалярна величина, також є розв’язком цієї системи.

Дійсно, за умовою

.

Але тоді і

оскільки дорівнює нулю вираз в дужках. Тобто є розв’язком однорідної системи.

Властивість 2. Якщо дві векторні функції 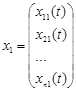,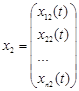є розв’язками однорідної системи, то і їхня сума також буде розв’язком однорідної системи.

Дійсно, за умовою

і

Але тоді і

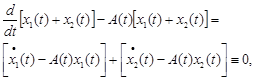
тому що дорівнюють нулю вираз в дужках, тобто є розв’язком однорідної системи.

Властивість 3. Якщо вектори 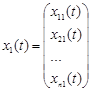, … , 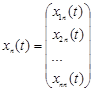є розв’язками однорідної системи, та і їхня лінійна комбінація з довільними коефіцієнтами також буде розв’язком однорідної системи.

Дійсно, за умовою

.

Але тоді і

тому що дорівнює нулю кожний з доданків, тобто є розв’язком однорідної системи.

Властивість 4. Якщо комплексний вектор з дійсними елементами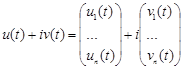є розв’язком однорідної системи, то окремо дійсна та уявна частини є розв’язками системи.

Дійсно за умовою

Розкривши дужки і зробивши перетворення, одержимо

А комплексний вираз дорівнює нулю тоді і тільки тоді, коли дорівнюють нулю дійсна і уявна частини, тобто

що і було потрібно довести.

Визначення 1. Вектори 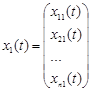, , 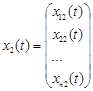… , 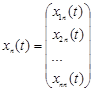називаються лінійно залежними на відрізку , якщо існують не всі рівні нулю сталі , такі, що при .

Якщо тотожність справедлива лише при , то вектори лінійно незалежні.

Визначення 2. Визначник, що складається з векторів

, тобто

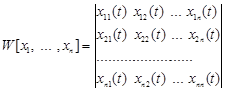
називається визначником Вронського.

Теорема 1. Якщо векторні функції лінійно залежні, то визначник Вронського тотожно дорівнює нулю.

Доведення. За умовою існують не всі рівні нулю , такі, що при .