Сторінка
1

Лінійна однорідна система з постійними коефіцієнтами. Застосування теорії диференціальних рівнянь в економіці

План

• Лінійна однорідна система диференціальних рівнянь з постійними коефіцієнтами
• Лінійна неоднорідна система диференціальних рівнянь з постійними коефіцієнтами
• Застосування теорії диференціальних рівнянь в економіці
• Модель природного випуску продукції
• Ріст випуску продукції в умовах конкуренції
• Динамічна модель Кейнса
• Неокласична модель росту
• Поняття про різницеві методи. Модель ділового циклу Самуельсона-Хікса

12.11. Лінійна однорідна система диференціальних

рівнянь першого порядку із сталими коефіцієнтами

Лінійна система диференціальних рівнянь із сталими коефіцієнтами має такий вигляд:

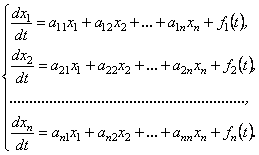(12.59)

Така система називається неоднорідною системою. Відповідна їй однорідна система лінійних диференціальних рівнянь із сталими коефіцієнтами має вигляд

(12.60)

Для запису нормальної системи диференціальних рівнянь з постійними коефіцієнтами зручно користуватися матричними позначеннями.

Позначимо ,

.

Тоді

,

і система (12.59) в матричних позначеннях набуває форми

(12.61)

Відповідна їй однорідна система має вигляд

(12.62)

Користуючись методом виключення, переходимо від системи рівнянь першого порядку до одного диференціального рівняння вищого порядку. Виявляється, що лінійне рівняння -го порядку завжди можна звести до системи рівнянь першого порядку. Нехай наприклад , диференціальне рівняння -го порядку дано у вигляді

. (12.63)

Введемо такі позначення:

.

Тоді з рівняння (12.103) випливає, що

.

Рівняння (12.103) можна подати у вигляді

,

де ,, - матриця розміру виду

Приклад . Записати диференціальне рівняння

у вигляді системи.

Введемо позначення: , , .

Тоді в силу умови маємо: . Рівняння зводиться до системи вигляду

Розглянемо однорідну систему диференціальних рівнянь (12.60), де коефіцієнти - сталі числа. Систему (12.60) можна звести до диференціального рівняння -го порядку з сталими коефіцієнтами. Але це робити не обов’язково. Є загальний метод розв’язування системи (12.60), який дозволяє наочніше досліджувати її розв’язки .

Ейлер запропонував шукати розв’язок системи (12.60) у вигляді

(12.64)

де - поки що невідомі сталі. Підставляючи в систему (12.60) рівності (12.64) та їх похідні й скоротивши на отримаємо

(12.65)

Зауважимо, що (12.65) - однорідна система лінійних алгебраїчних рівнянь відносно

Головний визначник системи

.

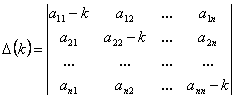З лінійної алгебри відомо, що у випадку, коли , система (12.65) має лише єдиний тривіальний (тобто нульовий) розв’язок.

Нетривіальні (ненульові) розв’язки існують лише тоді, коли .

Прирівняємо до нуля :

(12.66)

Рівняння (12.66) називається характеристичним рівнянням системи (12.60), а його корені - коренями характеристичного рівняння.