Сторінка
7

Лінійна однорідна система з постійними коефіцієнтами. Застосування теорії диференціальних рівнянь в економіці

(12.84)

де визначається за формулою (12.83).

Стаціонарний розв’язок цього рівняння має вигляд

Розглянемо конкретну задачу: для виробничої функції знайти інтегральні криві рівняння (12.84) і стаціонарний розв’язок. Із (12.83) випливає, що і тоді рівняння (12.84) має вигляд

(12.85)

Стаціонарний розв’язок цього рівняння випливає із рівності

звідки ми отримаємо ненульовий частинний розв’язок рівняння (12.137):

Відокремлюючи змінні в рівнянні (12.85), одержимо

Інтегруючи це рівняння (заміною ), одержимо загальний розв’язок рівняння

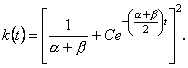(12.86)

Сімейство інтегральних кривих збігається зверху і знизу до стаціонарного розв’язку (рис.12.6): тобто при Отже, при незмінних вхідних параметрах задачі і функція фондоозброєності стійко прямує до стаціонарного значення незалежно від початкових умов. є точкою стійкої рівноваги.

12.13.5. Поняття про різницеві рівняння.

Модель ділового циклу Самуельсона-Хікса

Рівняння виду

(12.87)

де фіксоване, а довільне натуральне число, члени деякої числової послідовності, називається різницевим рівнянням го порядку.

Розв’язати різницеве рівняння означає знайти всі послідовності що задовольняють рівняння (12.87). Різницеві рівняння часто використовуються в моделях економічної динаміки з дискретним часом, а також для наближеного розв’язку диференціальних рівнянь.

Означення. Різницеве рівняння виду

(12.88)

де деякі функції від називається лінійним різницевим рівнянням го порядку.

У випадку, коли коефіцієнти є сталими, методи розв’язування такого класу рівнянь багато де в чому аналогічні

розв’язуванню лінійних диференціальних рівнянь з постійними коефіцієнтами. Проілюструємо це на прикладі різницевих рівнянь другого порядку:

(12.89)

Загальний розв’язок рівняння (12.89) визначається за формулою

де загальний розв’язок однорідного рівняння а деякий частинний розв’язок неоднорідного рівняння (12.89). Для знаходження загального розв’язку однорідного рівняння складаємо характеристичне рівняння

1) Якщо корені характеристичного рівняння дійсні і різні, то загальний розв’язок знаходиться за формулою

2) Якщо корені дійсні і рівні то

2) У випадку комплексних спряжених коренів загальний розв’язок має вигляд

Приклад. Розв’язати рівняння

Р о з в ‘ я з о к. Корені характеристичного рівняння

Тому загальний розв’язок однорідного рівняння

Частинний розв’язок неоднорідного рівняння шукаємо у вигляді Підставляючи цей вираз в наше рівняння, одержимо

Отже, і

Таким чином, загальний розв’язок рівняння має вигляд:

В якості прикладу, що ілюструє застосування різницевих рівнянь, розглянемо модель ділового циклу Самуельсона-Хікса (динамічний варіант моделі Кейнса). В цій моделі використовується так званий принцип акселерації, тобто припущення, що масштаби інвестування прямо пропорційні приросту національного доходу. Дане припущення характеризується рівнянням

(12.90)

де коефіцієнт фактор акселерації, величина інвестицій в період величини національного доходу відповідно в му і му періодах. Припускаємо також, що споживання на цьому етапі залежить від величини національного доходу на попередньому етапі, тобто