Сторінка
1

Лінійні диференціальні рівняння вищих порядків

Рівняння вигляду

називається лінійним неоднорідним диференціальним рівнянням -го порядку.

Рівняння вигляду

називається лінійним однорідним диференціальним рівнянням -го порядку.

Якщо при коефіцієнти неперервні, то для рівняння

виконуються умови теореми існування та єдиності і існує єдиний розв’язок , що задовольняє початковим умовам

.

1. Лінійні однорідні рівняння.

1.1. Властивості лінійних однорідних рівнянь

Властивість 1. Лінійність і однорідність зберігаються при довільному перетворенні незалежної змінної .

Дійсно. Після заміни, одержимо

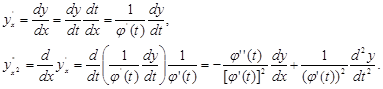
І після підстановки і приведення подібних, одержимо знову лінійне однорідне рівняння

.

Властивість 2. Лінійність і однорідність зберігаються при лінійному перетворенні невідомої функції .

Дійсно. Після заміни , одержимо

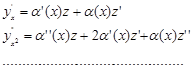
І після підстановки одержимо знову лінійне однорідне рівняння

.

1.2. Властивості розв’язків лінійних однорідних рівнянь

Властивість 1. Якщо є розв’язком однорідного лінійного рівняння, то і , де - довільна стала, теж буде розв’язком однорідного лінійного рівняння.

Дійсно. Нехай - розв’язок лінійного однорідного рівняння, тобто

.

Тоді і

оскільки вираз в дужках дорівнює нулю.

Властивість 2. Якщо і є розв’язками лінійного однорідного рівняння, то і теж буде розв’язком лінійного однорідного рівняння.

Дійсно. Нехай і - розв’язки лінійного рівняння, тобто

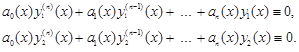
Тоді і

оскільки обидві дужки дорівнюють нулю.

Властивість 3. Якщо - розв’язки однорідного лінійного рівняння, то і , де - довільні сталі, також буде розв’язком лінійного однорідного рівняння.

Дійсно . Нехай - розв’язки лінійного однорідного рівняння, тобто

, .

Тоді і

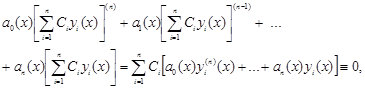
оскільки кожна дужка дорівнює нулю.

Властивість 4. Якщо комплексна функція дійсного аргументує розв’язком лінійного однорідного рівняння, то окремо дійсна частина і уявна будуть також розв’язками цього рівняння.

Дійсно. Нехайє розв’язком лінійного однорідного рівняння, тобто

Розкривши дужки і перегрупувавши члени, одержимо

Комплексний вираз дорівнює нулю тоді і тільки тоді, коли дорівнюють нулю дійсна і уявна частини, тобто

або функції є розв’язками рівняння, що і було потрібно довести.

1.3. Лінійна залежність і незалежність розв’язків. Загальний розв’язок лінійного однорідного рівняння вищого порядку

Визначення. Функції називаються лінійно залежними на відрізку якщо існують не всі рівні нулю сталі такі, що при всіх

Якщо ж тотожність справедлива лише , то функції називаються лінійно незалежними.

Приклад 3.1.1. Функції - лінійно незалежні на будь-якому відрізку , тому що вираз є многочленом ступеню і має не більш, ніж дійсних коренів.