Сторінка
2
Або, розписавши покоординатно, одержимо
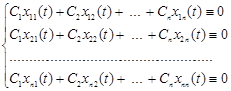 .
.
А однорідна система має ненульовий розв’язок ![]() тоді і тільки тоді, коли визначник дорівнює нулю, тобто
тоді і тільки тоді, коли визначник дорівнює нулю, тобто
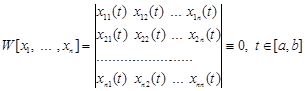 .
.
Теорема 2. Якщо розв’язки ![]() - лінійної однорідної системи лінійно незалежні, то визначник Вронського не дорівнює нулю в жодній точці
- лінійної однорідної системи лінійно незалежні, то визначник Вронського не дорівнює нулю в жодній точці ![]() .
.
Доведення. Нехай, від супротивного, існує точка![]() і
і ![]() .
.
Тоді система однорідних алгебраїчних рівнянь
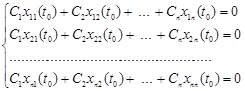
має ненульовий розв’язок ![]() . Розглянемо лінійну комбінацію розв’язків з отриманими коефіцієнтами
. Розглянемо лінійну комбінацію розв’язків з отриманими коефіцієнтами
![]() .
.
Відповідно до властивості 4, ця комбінація буде розв’язком. Крім того, як випливає із системи алгебраїчних рівнянь, для отриманих ![]() :
: ![]() ,
, ![]() . Але розв’язком, що задовольняють таким умовам, є
. Але розв’язком, що задовольняють таким умовам, є ![]() . І в силу теореми існування та єдиності ці два розв’язки збігаються, тобто
. І в силу теореми існування та єдиності ці два розв’язки збігаються, тобто ![]() при
при ![]() , або
, або
![]() ,
,
або розв’язки ![]() лінійно залежні, що суперечить умові теореми.
лінійно залежні, що суперечить умові теореми.
Таким чином, ![]() у жодній точці
у жодній точці ![]() , що і було потрібно довести.
, що і було потрібно довести.
Теорема 3. Для того щоб розв’язки ![]() були лінійно незалежні, необхідно і достатно, щоб
були лінійно незалежні, необхідно і достатно, щоб ![]() у жодній точці
у жодній точці ![]() .
.
Доведення. Випливає з попередніх двох теорем.
Теорема 4. Загальний розв’язок лінійної однорідної системи представляється у вигляді лінійної комбінації п -лінійно незалежних розв’язків.
Доведення. Як випливає з властивості 3, лінійна комбінація розв’язків також буде розв’язком. Покажемо, що цей розв’язок загальний, тобто завдяки вибору коефіцієнтів ![]() можна розв’язати будь-яку задачу Коші
можна розв’язати будь-яку задачу Коші ![]() або в координатній формі:
або в координатній формі:
![]() .
.
Оскільки розв’язки ![]() лінійно незалежні, то визначник Вронського відмінний від нуля. Отже, система алгебраїчних рівнянь
лінійно незалежні, то визначник Вронського відмінний від нуля. Отже, система алгебраїчних рівнянь
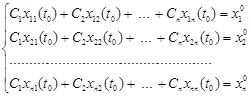
має єдиний розв’язок ![]() .
.
Тоді лінійна комбінація
![]()
є розв’язком поставленої задачі Коші. Теорема доведена.
Властивість 1. Максимальне число незалежних розв’язків дорівнює кількості рівнянь.
Це випливає з теореми про загальний розв’язок системи однорідних рівнянь, тому що будь-який інший розв’язок може бути представлений у вигляді лінійної комбінації ![]() лінійно незалежних розв’язків.
лінійно незалежних розв’язків.
Визначення. Матриця, складена з будь-яких ![]() -лінійно незалежних розв’язків, називається фундаментальною матрицею розв’язків системи.
-лінійно незалежних розв’язків, називається фундаментальною матрицею розв’язків системи.
Якщо лінійно незалежними розв’язками будуть
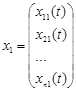 ,
, 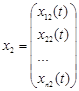 , … ,
, … , 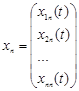 ,
,
то матриця
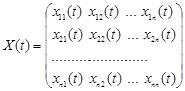
буде фундаментальною матрицею розв’язків.
Як випливає з попередньої теореми загальний розв’язок може бути представлений у вигляді
![]() ,
,
де ![]() - довільні сталі. Якщо ввести вектор
- довільні сталі. Якщо ввести вектор 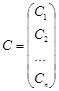 , то загальний розв’язок можна записати у вигляді
, то загальний розв’язок можна записати у вигляді ![]() .
.
2. Формула Якобі
Нехай ![]() - лінійно незалежні розв’язки однорідної системи,
- лінійно незалежні розв’язки однорідної системи, ![]() - визначник Вронського. Обчислимо похідну визначника Вронського
- визначник Вронського. Обчислимо похідну визначника Вронського
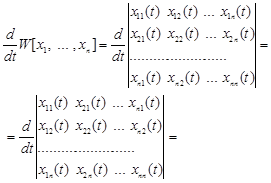
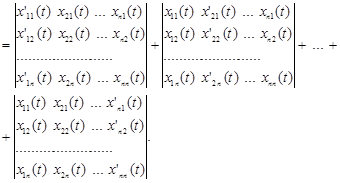
Інші реферати на тему «Математика»:
Частинні похідні і диференціали вищих порядків
Схеми застосування інтеграла до знаходження геометричних і фізичних величин. Обчислення площ плоских фігур в декартових і полярних координатах
Основні означення та факти з теорії визначників
Границя та неперервність функцій багатьох змінних
Задачі геометричного і фізичного змісту, що приводить до поняття подвійного інтеграла
