Сторінка
3
Оскільки для похідних виконується співвідношення
………………………………………….
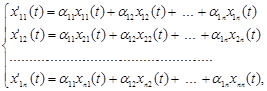
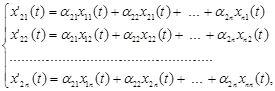
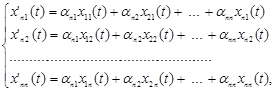
то після підстановки одержимо
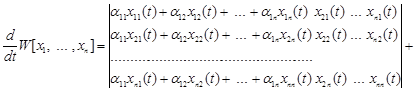
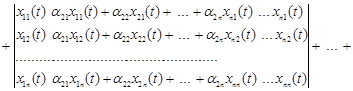
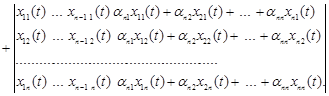
Розкривши кожний з визначників, і з огляду на те, що визначники з однаковими стовпцями дорівнюють нулю, одержимо
.
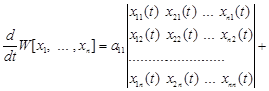
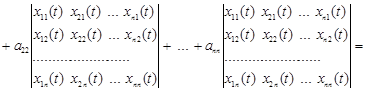
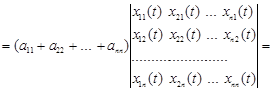
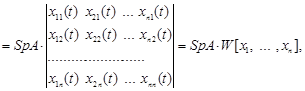
Або
.
Розділивши змінні, одержимо
.
Проінтегруємо в межах 
,
,
або
.
Взагалі кажучи, доведення проводилося в припущенні, що система рівнянь може залежати від часу, тобто
.
Отримана формула називається формулою Якобі.
Завантажити реферат