Сторінка
1

Визначені та невласні інтеграли

Визначений інтеграл є одним із основних понять математич­ного аналізу і широко використовується в різних галузях науки, техніки та в економічних дослідженнях.

1. Означення та властивості визначеного інтеграла

1.1. Задачі, що привели до поняття визначеного інтеграла

Розглянемо дві задачі — геометричну та фізичну.

1. Обчислення площі криволінійної трапеції. Нехай на відрізку [а, b] визначена неперервна функція у = f (х) і будемо поки що вважати, що f (х)0 для усіх x є [а, А].

Фігуру, обмежену кривою у = f (х), відрізком [а, b] осі 0х, прямими х = а та х = b, називають криволінійною трапецією (дивись Малюнок 1). В окремих випадках може f (а) = 0 або f (b) = 0 і тоді відповідна сторона трапеції стягується в точку.

Для обчислення площі S цієї криволінійної трапеції поділимо відрізок [а,b] довільним чином на n частин точками

а = х0 < x1 < х2 < . < xk < . < хn = b

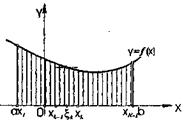Довжини цих частин

Перпендикуляри до осі 0х, проведені із точок ділення до перети­ну із кривою у = f (х), розділяють усю площу трапеції на n вузьких криволінійних трапецій. Замінімо кожну із цих трапецій прямокутника з основою та висотою , де . Площа кожного такого прямокутника дорівнює

Сума площ усіх таких прямокутників буде дорівнювати

Таким чином, площа S криволінійної трапеції наближено дорівнює цій сумі, тобто

Ця формула буде тим точнішою, чим менше величина .

Щоб одержати точну формулу для обчислення площі S криволінійної трапеції, треба в цій формулі перейти до границі, коли Тоді

(1)

2. Обчислення шляху, який пройшла точка. Нехай потрібно визначити шлях S, який пройшла матеріальна точка, що рухається в одному напрямі із змінною швидкістю V(t) за час від t0 до T.

Поділимо проміжок часу T-t0 на n частин: Δt1,Δt2,…,Δtn.

Позначимо через довільний момент часу із проміжку Δtk, а значення швидкості у цій точці позначимо .

Точка, що рухається з постійною швидкістю Vk на проміжку часу Δtk, проходить за цей час шлях а за час T - t0 вона пройде шлях

Будемо вважати, що шлях S, пройдений точкою, наближено дорівнює цій сумі. Коли Δtk→0, тоді змінна швидкість на проміжку Δtk мало відрізняється від постійної Vk. Тому дійсне значення шляху, пройденого точкою за час T - t0 буде дорівнювати границі цієї суми при max Δtk→ 0, тобто

(2)

До аналогічної суми зводиться задача про роботу змінної сили, що направлена по прямій лінії — траєкторії руху точки, до якої прикладена ця сила та інші задачі.

1.2. Означення визначеного інтеграла та його зміст

Нехай функція f (х) задана на відрізку [a, b]. Розіб'ємо цей відрізок на n частин точками ділення

а = х0 < x1 < x2 < . < хn = b

У кожному проміжку [xk-1, xk] довжиною Δхk = хk- хk-1 оберемо довільну точку і обчислимо відповідне значення функції .

Побудуємо суму яку називають інтегральною сумою для функції f (х) на відрізку [а,b].

Означення 1. Якщо існує скінченна границя інтегральної суми при , незалежна від способу ділення відрізка [а,b] на частини та добору точок , то ця границя називається визначеним інтегралом від функції f (х) на відрізку [а,b] і позначається

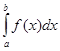
Математично це означення можна записати так:

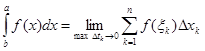(3)

Відмітимо, що числа а та b називають нижньою та верхньою межами, відповідно.

Згідно з цим означенням рівності (1) та (2) тепер можна за­писати у вигляді

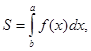
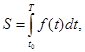(4)

тобто площа криволінійної трапеції S та шлях S, пройдений точкою із змінною швидкістю V = f (t) виражаються визначеним інтегралом. Перевірка існування скінченної границі інтегральної суми для кожної функції утруднена. Але такої перевірки робити не треба тому, що використовують таку відому теорему.

Теорема 1. Якщо функція f (х) неперервна на відрізку [а, b] або обмежена і має скінченну кількість точок розриву на цьому відрізку, то границя інтегральної суми існує, тобто функція f (х) інтегрована на [a, b].

1.3. Основні властивості визначеного інтеграла

Із означення (3) визначеного інтеграла та основних теорем про граниш випливають слідуючі властивості.