Сторінка
1

Задачі, що приводять до похідної. Визначення похідної, її геометричний і механічний зміст

План

• Задачі, що приводять до похідної.
• Означення похідної.
• Геометричний та механічний зміст похідної.
• Рівняння дотичної і нормалі до графіка кривої.
• Частинні похідні функції декількох змінних, їх геометричний зміст.

ДИФЕРЕНЦІАЛЬНЕ ЧИСЛЕННЯ. ФУНКЦІЇ ОДНІЄЇ ТА ДЕКІЛЬКОХ ЗМІННИХ

1. Вступні відомості

Нехай матеріальна точка рухається прямолінійно, а закон руху її задається деякою функцією

(6.1)

1. Поставимо задачу: знайти швидкість точки в момент часу .

Нехай в деякий момент часу точка займала положенням (рис.6.1).Через проміжок часу точка займе положення і пройде шлях .

Відношення

(6.2)

називається середньою швидкістю руху точки.

Означення. Швидкістю точки в момент часу називається границя середньої швидкості на проміжку часу , коли прямує до нуля:

(6.3)

Зазначимо, що формула дає змогу знайти швидкість у момент часу тільки тоді , коли існує границя цього відношення.

Рис.6.1

2. Задача про дотичну до кривої. З поняттям дотичної до кривої в даній точці ми зустрічалися при вивченні кола за шкільною програмою, за якою давалося означення дотичної до кола як прямої лінії, що має з колом одну спільну точку. Проте це означення є окремим випадком. Його не можна поширити, наприклад, на незамкнуті криві. Тому треба дати загальне означення дотичної, яке б підходило як до замкнутих, так і до незамкнутих кривих.

Нехай маємо деяку довільну криву (рис.6.2, 6.3). Візьмемо на цій кривій точки та і через них проведемо пряму , яку називатимемо січною. Якщо точка переміщатиметься вздовж кривої, то січна повертатиметься навколо . Нехай , рухаючись вздовж кривої, наближається до точки , тоді довжина хорди прямує до нуля. Якщо при цьому й значення кута прямує до нуля, то пряма називається граничним положенням січної .

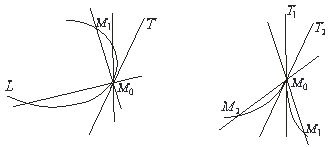
Рис.6.2 Рис.6.3

Означення. Дотичною до кривої в точці називається граничне положення січної , якщо точка прямує вздовж кривої до злиття з точкою .

Зауважимо, що яким би чином точка не наближалася по кривій до точки , січна повинна при цьому наближатися до того самого граничного положення (до тієї самої прямої). Тільки в цьому випадку кажуть, що в точці крива має дотичну. Граничне положення січної може не існувати.

Із рисунка (6.2) видно, з якого б боку точка по кривій не рухалася б до точки , січна , обертаючись навколо точки , при цьому наближається до тієї самої прямої . Якщо січна наближається до різних прямих (рис.6.3), залежно від того, з якого боку , то кажуть, що в даній точці