Сторінка
2

Визначені та невласні інтеграли

1 Постійний множник можна виносити за знак визначеного інтеграла, тобто якщо А — стала, то

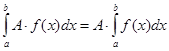
2 Визначений інтеграл від алгебраїчної суми скінченної кіль­кості функцій дорівнює такій самій алгебраїчній сумі інтегралів від кожного доданку, тобто

3 Якщо поміняти місцями межи інтегрування, то визначений інтеграл змінює свій знак на протилежний, тобто

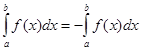
4 Визначений інтеграл з рівними межами дорівнює нулю, тобто

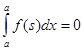
для будь-якої функції f (х).

5 Якщо f (х) (х), х [а, b], то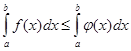

6 Якщо m та M — найбільше та найменше значення функції f (х) на відрізку [a,b], то

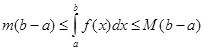
7 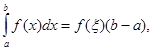де

8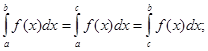

1.4. Обчислення визначених інтегралів

Раніше ми навчились знаходити невизначені інтеграли. Тому для обчислення визначених інтегралів доцільно встановити зв'язок між ними.

2.1. Зв'язок між визначеним та невизначеним інтегралами

Означення 2. Визначений інтеграл з постійною нижньою межею та змінною верхньою межею називають інтегралом із змінною верхньою межею.

Щоб мати звичне позначення, змінну верхню межу позначимо через х, а змінну інтегрування — t. Одержимо інтеграл

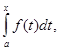який є функцієюх, тобто Ф(х) =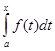

Теорема 2. Якщо f (х) неперервна функція, то похідна ви­значеного інтеграла від неперервної функції по змінній верхній межі дорівнює значенню підінтегральної функції для цієї верхньої межі, тобто

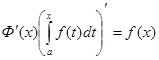(5)

Доведення. Надамо аргументу х приріст Δх, тоді функція Ф(х) одержить приріст, який згідно з властивістю 8 визначеного інтеграла можна записати у вигляді

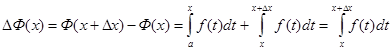
До останнього інтеграла застосуємо властивість 7, тоді

де

Згідно з означенням похідної маємо

що й треба було довести.

Теорема 3. Визначений інтеграл від неперервної функції дорівнює різниці значень будь-якої її первісної для верхньої та нижньої меж інтегрування, тобто якщо F(x) є первісна функції f (х), то має місце рівність ь

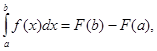(6)

яка називається формулою Ньютона-Лейбніца.

Доведення. Нехай F(x) деяка первісна функції f (х). За теоремою 2 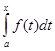також первісна для f (х). Але дві первісні функції f (х) відрізняються лише на постійний доданок С. Тому

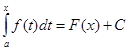(7)

Ця рівність (7) при відповідному обранні С буде тотожністю, тобто має місце для усіх х.

Для визначення С візьмемо у формулі (7) х = а. Тоді

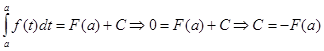
Отже,

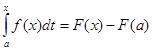
Якщо у цій рівності покласти х = b, то одержимо

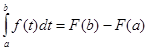
Змінюючи змінну інтегрування t на х, одержимо формулу (6), що й треба було довести.

Відмітимо, що різницю позначають часто так:

F(x) , тобто F(x)=

Тому формулу Ньютона-Лейбніца (6) можна записати у вигляді

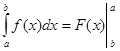
Ця формула вказує не тільки на зв'язок визначеного інтеграла з невизначеним, але й спосіб обчислення .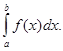

Приклад 1. Обчислити

Розв’язування.

2.2. Інтегрування частинами

Якщо проінтегрувати обидві частини рівності

d[u(x) · v(x)] = v(x)du(x) + u(x)dv(x)

в межах від а до b, то одержимо

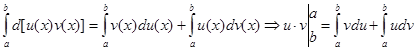
Звідси одержуємо важливу формулу інтегрування частинами визначеного інтеграла.

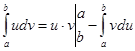(8)

Приклад 2. Обчислити інтеграл xcosxdx.

Розв'язування. Нехай u = x, dv = cosxdx , тоді знаходимо du = dx, 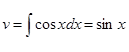(взята первісна без сталої С). Застосовуючи до заданого інтеграла формулу (8), одержимо

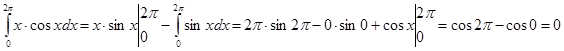
2.3. Заміна змінної у визначеному інтегралі

Теорема 4. Нехай задано інтеграл 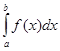, де f (х) неперервна на відрізку [а,b]. Зробимо підстановку х = (t), аtß, де (t) неперервно диференційована функція на відрізку [,ß].