Сторінка
1

Квадратичні форми, їх приведення до діагонального (канонічного) вигляду

План

• Квадратична форма, її канонічний вигляд.
• Зведення квадратичної форми до канонічного вигляду.
• Зведення загального рівняння лінії (поверхні) до канонічного вигляду.
• Модель Леонт’єва багатогалузевої економіки.
• Лінійна модель торгівлі.

Квадратичні форми і зведення їх до канонічного вигляду

Квадратична форма, її канонічний вигляд

Квадратичною формою називається однорідний многочлен другого степеня відносно змінних Квадратична форма має вигляд

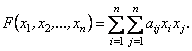(4.20)

причому - дійсні коефіцієнти.

Наприклад, квадратична форма двох змінних і має такий вигляд:

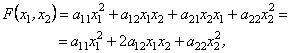
оскільки

Якщо через позначити матрицю а через матрицю-стовпчик то рівність (4.20) можна записати в матричній формі

(4.20/)

де

Через те, що в матриці , матриця є симетричною. Читачеві рекомендується перевірити формулу (4.20) звівши її до вигляду (4.19), користуючись явними записами матриць .

Симетрична матриця називається матрицею квадратичної форми. Якщо матриця має діагональний вигляд, то такий вигляд квадратичної форми називається канонічним виглядом.

Нехай тоді канонічний вигляд квадратичної форми буду таким:

(4.21)

Приведемо без доведення дві теореми про канонічний вигляд квадратичної форми ( доведення цих теорем див., наприклад, в підручнику Д.В.Беклемишева. Курс аналитической геометри и линейной алгебры ).

Теорема 1. Для кожної квадратичної форми існує базис, в якому вона має канонічний вигляд.

Теорема 2. (закон інерції квадратичних форм). Число додатних і від’ємних коефіцієнтів в канонічному вигляді квадратичної форми не залежить від вибору базису, в якому вона приведена до канонічного вигляду.

4.4.2. Зведення квадратичної форми до канонічного вигляду

У формулі (4.20/) виконаємо заміну , де , де

Матриця, обернена до якої співпадає з транспонованою, називається ортогональною.

Із заміни маємо ( при транспонуванні добутку матриць змінюється порядок перемноження матриць). Підставивши в (4.22) замість їх вирази, одержимо

де .

Отже, , де .

Теорема. Якщо матриця симетрична, то симетричною є і матриця .

Д о в е д е н н я. . Згідно з означенням симетричної матриці теж симетрична, що і треба було довести.

З теореми і заміни випливає, що є матрицею квадратичної форми, після заміни змінної. Оскільки - ортогональна матриця, тобто , то . Матрицю можна підібрати так (див.п.4.3.4, властивість 60), щоб

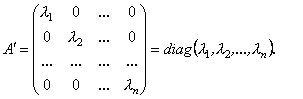(4.22)

Числа є власними значеннями матриці .

Якщо рівняння (4.19) має всі різні корені, то розв’язавши систему рівнянь (4.18) для кожного , одержимо взаємно ортогональних власних векторів:

Оскільки матриця - ортогональна, то , тобто

(4.23)

Зауваження. Після знаходження власних значень матриці із (4.19) і розв’язання системи рівнянь (4.18) одержимо власні вектори , які взагалі кажучи, не будуть одиничними. В такому разі з них можна одержати одиничні, поділивши кожний з них на його довжину Після такої операції уже будуть виконуватись умови (4.23). У нових змінних задана квадратична форма набуває вигляду