Сторінка
2

Векторна функція скалярного аргументу. Похідна, її геометричний і механічний зміст. Кривизна кривої

.

Формула диференціала дуги просторової кривої

. (7.10)

Приклад. Знайти диференціал дуги гвинтової лінії:

.

Р о з в ’ я з о к. .

.

Формулам (7.9) і (7.10) часто надають такого вигляду :

(для плоскої кривої); (7.11 (для просторової кривої); (7.12)

Диференціал дуги плоскої кривої має такий геометричний зміст: він дорівнює довжині відрізка дотичної до кривої (рис.7.5).

2.Кривизна плоскої кривої

Вивчаючи ту чи іншу криву, бачимо, що в різних точках вона має неоднаковий ступінь викривлення. Так, парабола поблизу початку координат більше викривлена, ніж в точках, які знаходяться далі від початку координат. Коло в усіх своїх точках має однакове викривлення. Різні криві також відрізняються одна від одної своїм ступенем викривлення. Коло малого радіуса більше викривлено, ніж коло великого радіуса.

Виникає запитання: що ж брати за міру кривизни кривої в її окремих точках? Щоб відповісти на нього, припустимо, що до кривої в кожній точці можна провести дотичну і що крива є спрямлюваною.

Візьмемо на кривій дві точки і (рис. 7.6) і в цих точках проведемо дотичні прямі. Нехай дотична утворює з додатним напрямом осі кут , а пряма - кут .

Довжину дуги позначимо . Модуль відношення , де - величина кута в радіанах, на який повертається дотична, коли точка переміститься вздовж кривої в точку , називається середньою кривизною дуги .

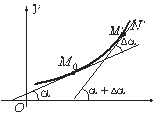
Рис.7.6

Означення. Границя (якщо вона існує) середньої кривизни дуги даної кривої, коли точка наближається вздовж кривої до точки , називається кривизною кривої в точці і позначається

. (7.13)

Виведемо формулу для обчислення кривизни. Нехай крива задана в декартовій системі координат рівнянням

,

де функція на відрізку має похідні до другого порядку включно.

Скористаємося формулою (7.13). Очевидно, що коли точка , то довжина дуги . Тому формулу (7.13) можна

записати ще так:

. (7.14)

З другого боку, якщо - кут, утворений дотичною до кривої в точці з додатним напрямом осі , то

.

Звідси

.

Тоді

.

Підставляючи в формулу (7.14) значення і значення , дістаємо формулу для кривини кривої:

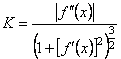. (7.15)

З цієї формули легко дістати формулу для кривизни кривої,

коли остання задана параметричними рівняннями . Справді,

,