Сторінка
1

Системи лінійних однорідних диференціальних рівнянь з сталими коефіцієнтами

Система диференціальних рівнянь вигляду

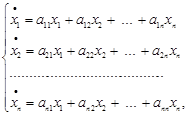
де - сталі величини, називається лінійною однорідною системою з сталими коефіцієнтами. У матричному вигляді вона записується

.

1. Розв’язування систем однорідних рівнянь з сталими коефіцієнтами методом Ейлера.

Розглянемо один з методів побудови розв’язку систем з сталими коефіцієнтами.

Розв’язок системи шукаємо у вигляді вектора

.

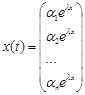Підставивши в систему диференціальних рівнянь, одержимо

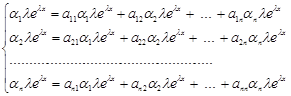
Скоротивши на , і перенісши всі члени вправо, запишемо

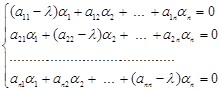
Отримана однорідна система лінійних алгебраїчних рівнянь має розв’язок тоді і тільки тоді, коли її визначник дорівнює нулю, тобто

.

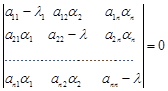Це рівняння, може бути записаним у векторно-матричній формі

і воно називається характеристичним (чи віковим) рівнянням. Розкриємо його

.

Алгебраїчне рівняння -го ступеня має -коренів. Розглянемо різні випадки.

1. Всі корені характеристичного рівняння (власні числа матриці ) дійсні і різні. Підставляючи їх по черзі в систему алгебраїчних рівнянь

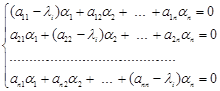
одержуємо відповідні ненульові розв’язки системи

, , … ,

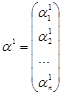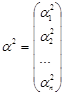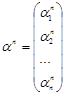
що являють собою власні вектори, які відповідають власним числам , .

У такий спосіб одержимо - розв’язків

, , … , .

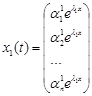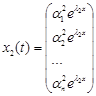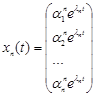Причому оскільки -різні а - відповідні їм власні вектори, то розв’язки - лінійно незалежні, і загальний розв’язок системи має вигляд

.

Або у векторно - матричної формі запису

,

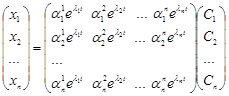де - довільні сталі.

2. Нехай пара комплексно спряжених коренів. Візьмемо один з них, наприклад . Комплексному власному числу відповідає комплексний власний вектор

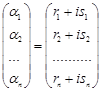
і, відповідно, розв’язок

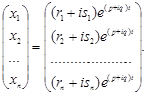
Використовуючи залежність , перетворимо розв’язок до вигляду:

.

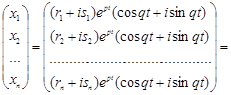
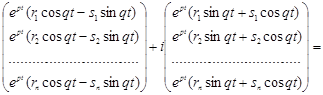
І, як випливає з властивості 4 розв’язків однорідних систем, якщо комплексна функція дійсного аргументу є розв’язком однорідної системи, то окремо дійсна і уявна частини також будуть розв’язками, тобто комплексним власним числам відповідають лінійно незалежні розв’язки

,.

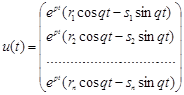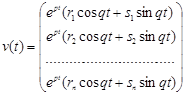3. Якщо характеристичне рівняння має кратний корінь кратності , тобто , то розв’язок системи рівнянь має вигляд

.

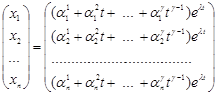Підставивши його у вихідне диференціальне рівняння і прирівнявши коефіцієнти при однакових степенях, одержимо - рівнянь, що містять -невідомих. Тому що корінь характеристичного рівняння має кратність , то ранг отриманої системи . Уводячи довільних сталих і розв’язуючи систему, одержимо

, , .

2. Розв’язок систем однорідних рівнянь зі сталими коефіцієнтами матричним методом

Досить універсальним методом розв’язку лінійних однорідних систем з сталими коефіцієнтами є матричний метод. Він полягає в наступному. Розглядається лінійна система з сталими коефіцієнтами, що записана у векторно-матричному вигляді

.

Робиться невироджене перетворення , де вектор - нова невідома векторна функція. Тоді рівняння прийме вигляд

або .

Для довільної матриці завжди існує неособлива матриця , що приводить її до жорданової форми, тобто , де - жорданова форма матриці . І система диференціальних рівнянь прийме вигляд