Сторінка
1

Побудова множинних фільтрів для лінійних алгебраїчних систем

В технічних задачах регулювання, при використанні теорії оптимального керування виникає необхідність у процедурах оцінювання і фільтрації. Оцінка стана системи керування або невідомих параметрів об'єкта є однією з важливих проблем у задачах керування і реставрації сигналу в цифровій обробці інформації. В даному параграфі побудований клас лінійних фільтрів [3] для оцінки параметрів об'єкта, що описується системою алгебраїчних рівнянь.

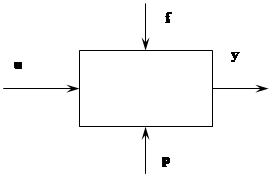
Загальна блок-схема системи з зображенням впливів на неї, її параметри і вимірювані дані про стан системи, зображені на малюнку.

Для даного малюнка введені наступні позначення:

u - керуючий вплив, що вибирається, значення якого відомі;

f - збурення, значення їх невідома, відомо апріорна множина можливих значень збурень;

p - параметр, у який може входити вектор стану системи, значення невідомі;

y - вимірювані дані про стан системи, значення відомі.

Зазначені дії на систему, параметри, вимірювані дані можуть бути скалярами, векторами, матрицями, функціями.

Рівняння математичної моделі системи керування у вищеописаних термінах має загальний вигляд

, (1)

де А - відома функція.

При прийнятій моделі невідомих шумів для системи, що описується рівнянням (1), можуть бути сформульовані наступні задачі:

Задача 1. Знайти при фіксованому u таку функцію , що має місце умова

(2)

У загальному випадку при фіксованому u існує множина таких функцій , яку будемо називати множиною фільтрів.

Задача 2. Знайти при фіксованому u оптимальну функцію згідно з умовою оптимальності

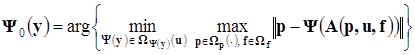. (3)

Множини , і функція будуються до проведення експерименту.

Розглянемо модель системи, що представлена у загальному випадку системою лінійних алгебраїчних рівнянь

, (4)

де матриця , вектори , , .

Матриця A і вектор d відомі параметри, досліджуваного об'єкта.

У випадку, коли відомо апріорна множина значень шумів f і маючи систему рівнянь, якій задовольняє вимірюваний вектор y, можна оцінити апостеріорну множину значень f і з використанням останньої і апріорної множини значень параметрів p оцінити апостеріорну повну множину значень параметрів.

Апостеріорна множина значень f (множина тих значень f , при котрих y може реалізуватися при деяких значеннях p відповідно до системи (4)) визначається таким чином

, (5)

де

,

- одинична матриця розмірності , - псевдообернена матриця, що визначається в такий спосіб [1]

.

Апостеріорна повна множина оцінюваних величин p (множина тих значень p, при яких реалізується вимірюваний вектор y і шум f, що належить множині значень (5)) визначається таким чином

, (6)

де , - одинична матриця розмірності n´n. Множина (6) записана з умови знаходження розв'язку [7] системи (4) відносно вектора p.

Для лінійної алгебраїчної системи, що описується рівнянням (1) розглянемо задачу 1. Рівняння (2), отримане на підставі (4) при буде мати вигляд

, (7)

де функцію виберемо лінійною наступного виду

, (8)

де - невідома матриця.

Якщо система (4) спостережна, тобто при з системи алгебраїчних рівнянь