Сторінка
1

Наближене розв’язування рівнянь: графічне відокремлення коренів, методи проб, хорд і дотичних

План

· Дотична і нормаль до плоскої кривої

· Наближене розв’язування рівнянь

• Графічне відокремлювання коренів
• Методи проб, хорд і дотичних
• Інтерполювання

ГЕОМЕТРИЧНІ ЗАСТОСУВАННЯ ДИФЕРЕНЦІАЛЬНОГО ЧИСЛЕННЯ.

НАБЛИЖЕНЕ РОЗВ’ЯЗУВАННЯ РІВНЯНЬ

1. Дотична і нормаль до плоскої кривої Якщо є рівняння кривої, а точка є точка дотику, то рівняння дотичної має вигляд

, (7.1) де . Пряма, яка проходить через точку дотику перпендикулярно до дотичної, називається нормаллю до кривої. Використаємо умову перпендикулярності двох прямих, тоді для нормалі одержимо рівняння

. (7.2) Приклади. 1. Скласти рівняння дотичної та нормалі до параболи в довільній її точці . Р о з в ’ я з о к. Диференціюємо рівняння параболи: , звідки , тому . Рівняння дотичної до параболи

; рівняння нормалі до параболи

. 2. Скласти рівняння дотичної та нормалі до циклоїди

. Р о з в ’ я з о к. Обчислюємо

. Рівняння дотичної до циклоїди в точці , що відповідає значенню параметра :

(дотична);

(нормаль). Дотична і нормаль кривої, побудовані в довільній її точці , в перетині з віссю утворюють прямокутний трикутник (рис. 7.1). Катети цього трикутника і та відрізки і часто використовуються в різних питаннях геометрії і дістали спеціальні позначення і назви:

- довжина дотичної;

- довжина нормалі;

- піддотична;

-піднормаль.

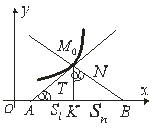
Рис.7.1 Ці відрізки можуть бути виражені через значення та в точці :

, або ;

, або ;

, або ;

, або . Враховуючи, що як , так і можуть мати від’ємні значення, одержані формули перепишемо:

. (7.3)

2. Наближене розв’язування рівнянь Розглянемо рівняння і нехай - його дійсний корінь, тобто Геометрично рівність означає, що графік функції проходить через точку осі Далі ми будемо розв’язувати задачу про знаходження з наперед заданою точністю наближеного значення кореня рівняння Спочатку розглянемо питання про відокремлення коренів рівняння. Корінь рівняння відокремлений, якщо знайдено відрізок ( позначимо його ), в якому, крім , немає інших коренів цього рівняння. Задача відокремлення коренів рівняння розв’язується просто, якщо побудова графіка функції не є важкою. Дійсно, маючи графік функції , легко виділити відрізки, в кожному із яких знаходиться лише один корінь розглядуваного рівняння, або, що те саме, виділити відрізки, на кожному із яких є лише одна точка перетину кривої з віссю Відділити корені рівняння при умові, що - диференційована функція, можна не лише графічно. Нехай на кінцях деякого відрізка функція має значення різних знаків. Тоді за властивістю неперервних функцій ця функція на інтервалі по меншій мірі один раз обертається в нуль, тобто рівняння має по меншій мірі один корінь. Якщо похідна зберігає знак на відрізку , то внаслідок монотонності функції рівняння на інтервалі має єдиний корінь. У цьому випадку числа та є наближеними значеннями кореня відповідно з нестачею і з надлишком. Ці інтервали можна звужувати, тоді границі їх будуть давати все точніші наближення для коренів рівняння. Нехай корінь рівняння відокремлений, тобто є відрізок , на якому, крім , немає інших коренів цього рівняння. Відшукаємо значення з будь-якою точністю за таких допущень: функція має на відрізку неперервні похідні до другого порядку включно і, крім того, похідні і зберігають знаки на цьому відрізку. Із цих умов випливає, що - монотонна функція на відрізку , яка на кінцях має різні знаки, а також, що крива опукла або вгнута (рис.7.2).