Сторінка
2

Побудова множинних фільтрів для лінійних алгебраїчних систем

вектор p знаходиться однозначно, то з представлення (8)

одержуємо умову , з якого матриця знаходиться наступним способом

, (9)

де псевдообрнена до матриці A, ,

- одинична матриця розмірності .

Таким чином, у класі лінійних функцій множина фільтрів лінійної алгебраїчної системи, що описується системою рівнянь (4), має вид

. (10)

У випадку присутності шуму f множина фільтрів (10) породить множину конкуруючих оцінок

(11)

Якщо система (4) не спостережувана при f=0. Тоді для системи

вектор p знаходиться неоднозначно

. (12)

Тоді у випадку присутності шуму f , без обмеження загальності в (12) покладемо , множина конкуруючих оцінок має вигляд

.

Тому що [5] , тоді

.

Таким чином формула (12) має загальний зміст.

Для множинних фільтрів при фіксованому u визначимо оптимальну функцію згідно до умови оптимальності

(13)

Множини , і функція будуються до проведення експерименту.

Тоді умова (13) визначає оптимальне значення матриці таким чином

. (14)

Будемо припускати, що мінімум і максимум досягаються.

Якщо f є випадковим векторною величиною з функцією розподілу , то тоді матрицю W можна вибрати оптимально згідно з імовірнісною умовою

,

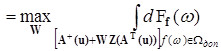або середньоквадратичною умовою

, (15)

де - допустима множина відхилень оцінки вектора від вектора параметрів, - кореляційна матриця вектора випадкових величин.

У загальному випадку умова мінімуму (15) досягається неоднозначно, тому вся множина оптимальних фільтрів при середньоквадратичній умові оптимізації має вигляд

, (16)

де матриця задовольняє умові .