Сторінка
1

Однорідні рівняння

1. Загальна теорія

Нехай рівняння має вигляд

.

Якщо функції та однорідні одного ступеня, то рівня­ння називається однорідним. Нехай функції та однорідні ступеня , тобто

Робимо заміну . Після підстановки одержуємо

,

або

.

Скоротивши на і розкривши скобки, запишемо

.

Згрупувавши, одержимо рівняння зі змінними, що розділяються

,

або

.

Взявши інтеграли та замінивши , отримаємо загальний інтеграл .

2. Рівняння, що зводяться до однорідних

Нехай маємо рівняння вигляду

.

Розглянемо два випадки

1) .

Тоді система алгебраїчних рівнянь

має єдиний розв’язок . Проведемо заміну та отримаємо

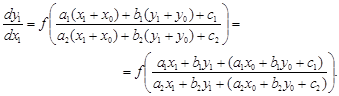
Оскільки - розв’язок системи алгебраїчних рівнянь, то диференціальне рівняння прийме вигляд

і є однорідним нульового ступеня. Робимо заміну .

Підставимо в рівняння

.

Одержимо

.

Розділивши змінні, маємо

.

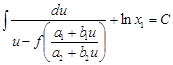І загальний інтеграл диференціального рівняння має вигляд .

Повернувшись до вихідних змінних, запишемо

.

2) Нехай , тобто коефіцієнти строк лінійно залежні і

.

Робимо заміну . Звідси .

Підставивши в диференціальне рівняння, одержимо

,

або

.

Розділивши змінні, отримаємо

.

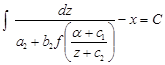Загальний інтеграл має вигляд