Сторінка
5

Теореми Ролля, Лагранжа, Коші. Правило Лопіталя. Формула Тейлора для функції однієї та двох змінних

Знайдемо границю показника:

тому

7.Маємо невизначеність виду . Запишемо даний вираз:

. Дістали невизначеність .

Отже,

.

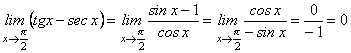8. Маємо невизначеність виду . Запишемо даний вираз:

.

Знайдемо границю показника:

.

Отже,

6.14. Формула Тейлора

6.14.1. Формула Тейлора для многочлена

Нехай задано многочлен

де - довільні дійсні числа, які називаються коефіцієнтами многочлена.

Виразимо коефіцієнти даного многочлена через значення многочлена та його похідні.

З цією метою будемо послідовно диференціювати многочлен. Матимемо

. . . . . . . . . . . . . . . . . . . .

Підставляючи в ці рівності , дістаємо

. . . . . . . . . .

Тоді многочлен набуде вигляду

(6.76)

Може трапитися, що многочлен буде записаний за степенями різниці , де - довільне дійсне число:

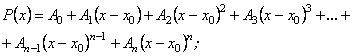
- дійсні числа. Тоді многочлен можна записати так:

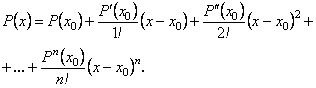(6.77)

Формулу (6.77) називають формулою Тейлора для многочлена.

6.14.2. Формула Тейлора для довільної функції

Візьмемо довільну функцію , яка в околі деякої точки і в самій точці має похідні до -го порядку включно.

Тоді для такої функції можна побудувати многочлен

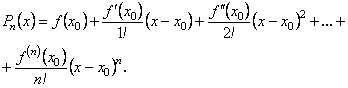(6.78)

Цей многочлен називається многочленом Тейлора для функції

Розглянемо таку різницю:

Оскільки залежить від то й залежить від

Тоді

або

(6.79)

Формула (6.79) називається формулою Тейлора для функції а функція - залишковим членом формули Тейлора.

Отже, формула Тейлора (6.79) відрізняється від формули Тейлора (6.77) для многочлена тим, що вона містить залишковий член Виразимо через похідну -го порядку від функції

Теорема. Якщо в деякому околі, наприклад, на відрізку точки має неперервні похідні до -го порядку включно, то залишковий член у формулі Тейлора можна записати у вигляді