Сторінка
3

Теореми Ролля, Лагранжа, Коші. Правило Лопіталя. Формула Тейлора для функції однієї та двох змінних

Д о в е д е н н я. Позначимо різницю через : .

Тоді функція на проміжку має похідну :

.

Проте , тому . Звідси випливає, що або, що те саме, .

6.12.3. Теорема Коші

Теорема. Нехай: 1) функції і задані і неперервні на відрізку ; 2) диференційовані в інтервалі ; 3) похідна всередині інтервалу не дорівнює нулю. Тоді всередині інтегралу знайдеться така точка , що має місце рівність

. (6.75)

6.13. Розкриття невизначеностей. Правило Лопіталя

Розглянемо невизначеність виду .

Теорема 1. Нехай для функцій і виконуються умови:

1) функції визначені на півінтервалі і

;

2) в інтервалі диференційовані, причому для всіх ;

3) існує (скінчена або нескінченна ) границя

.

Тоді існує границя відношення при і ця границя дорівнює теж числу , тобто

.

Висновок цієї теореми читають ще так: границя відношення функції дорівнює границі відношення похідних від цих функцій.

Наведену теорему називають першим правилом Лопіталя.

Зауваження 1. Може статися, що поряд з рівностями виконуються рівності

Нехай

тоді, застосовуючи двічі доведену теорему, дістаємо таку рівність:

Взагалі цей спосіб можна застосовувати доти, поки не прийдемо до відношення яке має при певну границю. Тоді

У цьому випадку кажуть, що правило Лопіталя використовується разів.

Зауваження 2. Теорема 1 при виконанні її умов справджується і тоді, коли точка є невласною, тобто . У цьому випадку

Справді, застосувавши підстановку , маємо

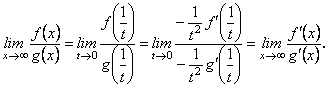
Сформулюємо другу теорему Лопіталя, яка стосується розкриття невизначеності виду

Теорема 2. Нехай для функцій і виконуються умови:

1) функції визначені на півінтервалі і при цьому

2) функції диференційовані в інтервалі причому

3) існує ( скінчена або нескінченна) границя

Тоді

.

Зауваження 3. Крім невизначеностей є ще й інші невизначеності: Проте всі вони зводяться до невизначеності або