Сторінка
6

Теореми Ролля, Лагранжа, Коші. Правило Лопіталя. Формула Тейлора для функції однієї та двох змінних

(6.80)

де

Формула (6.79) записується тепер у вигляді

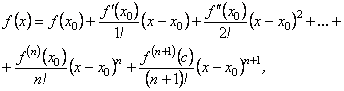(6.81)

і справедлива для будь-якого

Формула (6.81) називається формулою Тейлора із залишковим членом виду Лагранжа. Якщо в цій формулі покласти , то матимемо так звану формулу Маклорена

(6.82)

Враховуючи вирази для диференціалів різних порядків функції можна записати формулу (6.81) в диференціальній формі:

(6.83)

6.14.3. Формула Тейлора для функції двох змінних

Нехай функція має в околі точки неперервні частинні похідні до -го порядку включно. Формулу Тейлора зручно записати в диференціальній формі:

(6.84)

де

Аналогічний вигляд має формула Тейлора для функції більшого числа змінних.