Сторінка
4

Теореми Ролля, Лагранжа, Коші. Правило Лопіталя. Формула Тейлора для функції однієї та двох змінних

Справді, нехай, наприклад, маємо невизначеність Інакше кажучи, нехай маємо функції і такі, що Тоді добуток можна зобразити у вигляді частки: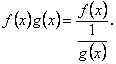

Отже, у правій частині ми маємо невизначеність виду

Якщо маємо невизначеність , тобто і то різницю можна записати:

отже, в правій частині маємо невизначеність виду

Якщо маємо степінь і тобто невизначеність виду , то її розкривають так.

Припускаючи, що , вираз має вигляд

У показнику при маємо невизначеність виду , яка (це було показано вище) зводиться до невизначеності . Аналогічно невизначеності розкриваються невизначеності , .

Приклади. Користуючись теоремами Лопіталя, знайти границі функцій:

1. 2. 3.

4. 5. 6.

7. 8.

Р о з в ’ я з о к. Перевіримо виконання умов теорем Лопіталя для першого прикладу. Для прикладів пропонуємо умови теорем перевірити самостійно.

1. Нехай . Розглядатимемо пів інтервал, де - довільне число. Тоді . Знаходимо похідні за будь-якого , а потім

.

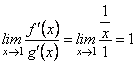Отже, виконуються всі три умови першої теореми Лопіталя. Тому

.

2. Маємо невизначеність виду . Використавши першу теорему Лопіталя, одержимо

.

3. Маємо невизначеність виду , тому використовуємо другу теорему Лопіталя:

.

4. Маємо невизначеність виду . Зводимо її до невизначеності . Для цього запишемо у вигляді

.

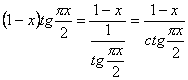Отже, дістали невизначеність . Тому

.

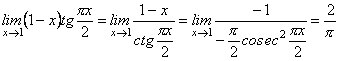5. Маємо невизначеність . Запишемо добуток

так: . Дістали невизначеність . Тому

Під знаком границі в правій частині останньої рівності знову маємо випадок, коли чисельник і знаменник прямують до , тобто маємо ту саму невизначеність . Застосувавши раз друге правило Лопіталя, дістаємо

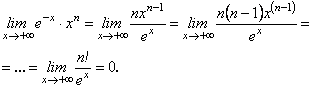
6. Маємо невизначеність . Тоді