Сторінка
2

Диференціал функції, його геометричний зміст. Лінеаризація функції

2. , .

3. , .

4. , .

5. , .

6. , .

7. , .

8. , .

9. , .

10. , .

11. , .

12. , .

13. , .

14. , .

15. , .

16. , .

17. , .

18. , .

Властивості диференціала. Якщо і - диференційовані функції, то безпосередньо із визначення диференціала і властивостей похідних маємо такі властивості диференціала:

1) (),

2) ,

3) ,

4) .

Геометричний зміст диференціала. Нехай графік диференційованої функції має вигляд, зображений на рис. 6.6 (крива ).

Візьмемо на кривій точки і . У точці проведемо дотичну до кривої . Тоді з трикутника знайдемо довжину відрізка :

або

. (6.53)

Рівність (6.53) і характеризує геометричний зміст диференціала: диференціал функції дорівнює приросту ординати дотичної до графіка цієї функції в розглядуваній точці.

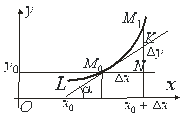
Рис.6.6

Механічний зміст диференціала. Припустимо, що матеріальна точка рухається за відомим законом

де - диференційована функція при деякому значенні часу . Тоді функція має диференціал

,або .

Добуток виражає шлях, який точка проходить за час , рухаючись із сталою швидкістю .

Отже, механічне тлумачення диференціала функції таке: диференціал функції виражає той шлях, який точка пройшла б за час , якби вона рухалася прямолінійно і рівномірно зі сталою швидкістю .

6.6.3. Повний диференціал функції двох змінних

Означення повного диференціала. Нехай функція в деякій області неперервна і має частинні похідні та .

Виберемо в цій області довільну точку . Надамо приросту обом аргументам, тобто візьмемо точку

. Для приросту