Сторінка
3

Диференціал функції, його геометричний зміст. Лінеаризація функції

одержуємо такий вираз:

(6.54)

При і останні два доданки є нескінченно малими вищого порядку, оскільки і . Перших два доданки складають головну частину у виразі повного приросту .

Означення. Головна, лінійна відносно і частина приросту функції називається повним диференціалом функції двох змінних і позначається або :

. (6.55)

(Легко бачити, що це означення приводить до введеного вище поняття диференціала функції однієї змінної, якщо замість розглядати функцію ).

Приклад. Знайти повний диференціал функції .

Р о з в ’ я з о к.

В будь-який точці .

Зауваження. Означення повного диференціала легко узагальнюється на випадок диференційованої функції будь-якого числа змінних.

Повним диференціалом функції в даній точці називається головна, лінійна відносно приросту всіх аргументів частина повного приросту функції.

Приклад. .

Р о з в ' я з о к.

В будь-які й точці

.

Означення дотичної площини і нормалі до поверхні. Є кілька еквівалентних між собою означень дотичної площини до поверхні. Ми дамо означення, яке є природним узагальненням означення дотичної (прямої) до кривої (рис. 6.7).

Нехай - точка даної поверхні. Розглянемо на поверхні другу, змінну точку і проведемо січну пряму .

Площина, що проходить через точку , називається дотичною площиною до поверхні в точці , якщо кут між січною і цією площиною прямує до нуля, коли віддаль прямує до нуля, яким би чином точка на поверхні не прямувала б до точки .

Нормаллю до поверхні в точці називається пряма, що проходить через точку перпендикулярно до дотичної площини до поверхні в цій точці.

Рівняння дотичної площини і нормалі. У поверхні, заданої рівнянням , де - функція, диференційована в точці , дотична площина в точці існує і має рівняння

. (6.56)

За рівнянням дотичної площини до поверхні в точці легко записати рівняння нормалі:

. (6.57)

Геометричний зміст повного диференціала. Нехай функція диференційована в точці . Це означає, що поверхня, задана рівнянням , має в точці дотичну площину (рис. 6.8). Її рівняння (6.56),

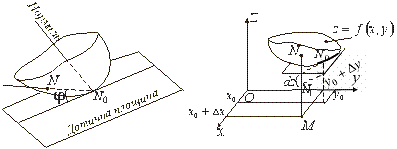
Рис.6.7 Рис.6.8

поклавши ; , можна записати у вигляді

.

У цьому рівнянні зліва стоїть різниця аплікат точок дотичної площини, відповідних точкам і , а справа – повний диференціал функції в точці .

Отже, повний диференціал функції в точці геометрично означає приріст аплікати дотичної площини до поверхні, яка зображує функцію, в точці при переході із точки в точку .

Інваріантна форма запису диференціала. За означенням, для диференційованої в точці функції двох незалежних змінних

.

Покладемо, зокрема, (тобто ), одержимо Отже, . Аналогічно, поклавши , одержимо . Таким чином, диференціали незалежних змінних співпадають з приростом цих змінних, і ми можемо записати диференціал функції у вигляді