Сторінка
1

Лінійні диференціальні рівняння другого порядку з постійними коефіцієнтами

План

• Лінійні неоднорідні диференціальні рівняння з постійними коефіцієнтами та правою частиною спеціального вигляду
• Права частина виду
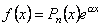
• Права частина виду

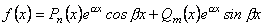
1. Лінійні неоднорідні рівняння другого порядку з постійними коефіцієнтами

Розглянемо диференціальне рівняння

(12.46)

в якому - дійсні числа, а - функція спеціального виду

(12.47)

де - многочлени -го і -го степеня, - дійсні числа. Виявляється, що це рівняння можна досить легко розв’язати, не вдаючись до методу варіації довільних сталих і навіть без інтегрування. Це надзвичайно важливо, бо багато практичних задач зводиться саме до такого рівняння.

1. Для простоти розглянемо спочатку частинний випадок функції (12.47), коли :

.

Тоді рівняння (12.70) набуває вигляду

(12.48)

Його загальний розв’язок як відомий з п.12.9 є сумою загального розв’язку відповідного однорідного рівняння та частинного розв’язку неоднорідного рівняння: З’ясовуємо, що вигляд частинного розв’язку залежить від того, збігається чи ні число з коренями характеристичного рівняння (12.39).

а). Нехай число не є коренями характеристичного рівняння (12.39): Тоді частинний розв’язок слід шукати у вигляді

(12.49)

де - многочлен -го степеня відносно з невизначеними коефіцієнтами :

Систему для визначення цих коефіцієнтів отримують після підстановки функції (12.49) у рівняння (12.48). Справді, така підстановка приводить до рівняння

Зліва й справа від знака рівності стоять многочлени -го степеня, бо многочлен -го степеня, причому а - многочлени відповідно 1-го і 2-го степеня. Прирівнюючи коефіцієнти при однакових степенях зліва й справа рівності отримаємо алгебраїчну систему рівнянь з невідомими

б). Нехай число є однократним (простим) коренем характеристичного рівняння (12.39): У цьому разі і зліва в рівності фігурує многочлен 1-го степеня. Ця рівність не є тотожністю при жодних сталих

Тому частинний розв’язок у цьому разі шукатимемо у формі

(12.50)

в). Нехай число є двократним коренем характеристичного рівняння Зауважимо, що в разі збігу коренів характеристичного рівняння маємо Якщо то виконується рівність Це означає, що зліва у рівності фігурує многочлен 2 -го степеня з невизначеними коефіцієнтами. Щоб отримати многочлен го степеня, слід шукати частинний розв’язок у вигляді

(12.51)

Приклад 1. Розв’язати рівняння

Р о з в ‘я з о к. Загальний розв’язок відповідного однорідного рівняння було знайдено в прикладі 1 а) п.12.9: