Сторінка
5

Числові послідовності. Границя, основні властивості границь

Теорема 1. Алгебраїчна сума двох збіжних послідовностей і є збіжна послідовність, її границя дорівнює відповідній сумі границь даних послідовностей.

Д о в е д е н н я. Нехай Тоді

де і - нескінченно малі послідовності.

Додавши почленно ці рівності, дістанемо:

Отже, вираз ми подали у вигляді суми сталого числа

і нескінченно малої Тому існує та

Зауваження . Теорема справедлива й для випадку всякого скінченого числа збіжних числових послідовностей.

Теорема 2. Добуток двох збіжних послідовностей і є збіжна послідовність, її границя дорівнює добутку границь даних послідовностей.

Д о в е д е н н я. За умовою теореми

Тому де - нескінченно малі послідовності.

Тоді

Із властивостей нескінченно малих виводимо, що послідовність

- нескінченно мала.

Звідси

тобто

Теорему доведено.

Зауваження. Теорема справедлива й у випадку добутку всякого скінченого числа збіжних послідовностей.

Наслідок 1. Якщо послідовність має скінчену границю, то при всякому сталому маємо:

або сталий множник можна виносити за знак границі.

Наслідок 2. Якщо і - натуральне число,

то

Теорема 3. Якщо послідовності і збігаються, причому і то

послідовність збігаються і її границя дорівнює відношенню

границь послідовностей та

Д о в е д е н н я. За умовою теореми

де - нескінченно малі послідовності.

Оскільки то де - стале число.

Надалі обмежимося тими членами послідовності які задовольняють попередній нерівності. Тоді

.

Послідовність є обмежена, оскільки

Послідовність є нескінченно мала. Таким чином, 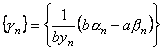є нескінченно мала.

Тому

Теорему доведено.

При вивчені основних теорем про границі ми вважали, що числові послідовності і мають скінченні границі, причому при доведенні теореми про границю частки вважали, що границя дільника не дорівнює нулю.

Розглянемо випадок, коли і є нескінченно великі числові послідовності, тобто

Легко бачити, що арифметична сума і добуток цих послідовностей є також нескінченно велика числова послідовність. Проте нічого конкретного в загальному випадку не можна сказати про частку від ділення та різницю цих послідовностей. Частка від ділення таких послідовностей залежно від закону зміни і може

поводити себе по-різному. Кожного разу відношення треба досліджувати. Тому говорять, що відношення якщо є невизначеність. І цю невизначеність символічно позначають так: