Сторінка
7
Знайдемо
![]() .
.
Отже, функції ![]() і
і ![]() на нескінченності однакового порядку малості.
на нескінченності однакового порядку малості.
3. Нехай ![]() ,
,
![]() і
і ![]() .
.
Знайдемо
![]() .
.
Отже, функції ![]() і
і ![]() при
при ![]() нескінченно малі однакового порядку малості.
нескінченно малі однакового порядку малості.
Означення 2. Якщо
![]() ,
,
то ![]() називається нескінченно малою вищого порядку малості, ніж
називається нескінченно малою вищого порядку малості, ніж ![]() . При цьому
. При цьому ![]() - нескінченно мала нижчого порядку малості, ніж
- нескінченно мала нижчого порядку малості, ніж ![]() .
.
Приклади.
1. Нехай ![]()
![]() . Тоді
. Тоді ![]() і
і ![]() в
в
точці ![]() є нескінченно малі функції. Знайдемо
є нескінченно малі функції. Знайдемо
![]()
Отже, в цьому випадку ![]() є нескінченно мала вищого порядку, ніж
є нескінченно мала вищого порядку, ніж ![]() .
.
2. ![]() ,
, ![]() ,
, ![]() і
і ![]() - нескінченно малі при
- нескінченно малі при![]() . Знайдемо
. Знайдемо
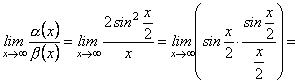

Отже, при ![]()
![]() є нескінченно мала вищого порядку, ніж
є нескінченно мала вищого порядку, ніж ![]() .
.
Означення 3. Якщо
![]() ,
,
то ![]() називається нескінченно малою більш нижчого порядку малості, ніж
називається нескінченно малою більш нижчого порядку малості, ніж ![]() .
.
Приклад.
Нехай ![]() ,
, ![]() . При
. При ![]()
![]() і
і ![]() - нескінченно малі. Знайдемо
- нескінченно малі. Знайдемо

Отже, при ![]()
![]() є нескінченно малою нижчого
є нескінченно малою нижчого
порядку малості, ніж ![]() .
.
Означення 4. Якщо границі відношення ![]() і
і ![]() не існує (ні скінчена, ні нескінченна), то
не існує (ні скінчена, ні нескінченна), то ![]() і
і ![]() називаються не порівнювальними нескінченно малими.
називаються не порівнювальними нескінченно малими.
Означення 5. Якщо
![]() ,
,
то ![]() і
і ![]() в точці
в точці ![]() називаються еквівалентними, і записуються :
називаються еквівалентними, і записуються : ![]() ~
~ ![]() .
.
Приклади.
1. Нехай ![]() ,
, ![]() . Тоді
. Тоді ![]() і
і ![]() в точці є нескінченно малі. Оскільки
в точці є нескінченно малі. Оскільки ![]() (доведення буде дано в наступній темі), то
(доведення буде дано в наступній темі), то ![]() і
і ![]() є еквівалентні величини, тобто
є еквівалентні величини, тобто ![]() ~
~ ![]() .
.
2. Довести, що в точці ![]() :
:
|
а) |
|
б) |
|
|
в) |
|
г) |
|
|
д) |
|
е) |
|
|
ж) |
|
з) |
|
Інші реферати на тему «Математика»:
Загальний розв'язок задачі термінального керування і спостереження
Диференціальні рівняння першого порядку, не розв’язані відносно похідної
Задачі, що приводять до похідної. Визначення похідної, її геометричний і механічний зміст
Існування та єдиність розв’язків диференціальних рівнянь першого порядку. Неперервна залежність та диференційованість
Джерела статистики, види середніх та способи їх обчислення
