Сторінка
1

Маса лінії. Координати центра ваги плоскої кривої та фігури

План

• Маса плоскої лінії
• Статичні моменти і центр ваги
• Обчислення моментів інерції
• Обчислення роботи
• Деякі задачі прикладного характеру

1. Застосування інтегрального числення у фізиці,

механіці, техніці

1.1. Маса плоскої лінії

У класичній механіці матеріальні тіла часто зображують як просторову область , що заповнена без прогалин речовиною. Якщо відома маса тіла і об’єм тієї області , яку вона заповнює, то відношення маси до називається середньою густиною . Часто доводиться мати справу з тілами, в яких густина в околі різних точок різна. Тоді густина буде функцією точки , що належить області , тобто . Якщо розглянути нескінченно малу область , що оточує точку , об’єм якої дорівнює , маса – , то . Звідки

.

У випадку, коли є функцією лише однієї змінної, наприклад , а (саме цей випадок тут і розглядатиметься), то

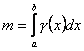, (10.13)

де .

Якщо розглядати матеріальну плоску криву з лінійною густиною розподілу мас то маса елементарного кусочка кривої буде звідки одержимо формулу для обчислення маси кривої

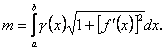(10.14)

1.2. Статичні моменти і центр ваги

Визначення. Статичним моментом матеріальної точки маси відносно осі (площини) називається добуток маси точки на її відстань 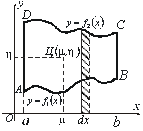від осі (площини) :.

Про статичний момент відносно осі говорять лише тоді, коли система матеріальних точок (неперервна або дискретна) є плоскою, тобто знаходиться в одній і тій самій площині, що й вісь. Якщо ж система матеріальних точок не належить одній площині, то мова може йти лише про статичний момент відносно площини.

Для системи матеріальних точок мас статичний момент відносно осі (площини) визначається сумою , де – відстані зі знаком ”+” або “-” залежно від того, де знаходяться точки (для точок, що лежать з одного боку від осі (площини) береться, наприклад, знак “+”, тоді для точок, що лежать з іншого боку, знак “-”).

Нехай у прямокутній системі координат задана неперервна плоска система матеріальних точок (лінія ) або плоска фігура . Густина (лінійна для лінії, поверхнева для фігури) є функцією однієї змінної, наприклад , тобто

Виділивши на лінії елемент дуги, віддалений від осі на відстань (від осі на відстань ) знайдемо елементарні статичні моменти відносно осей і :