Сторінка
2

Маса лінії. Координати центра ваги плоскої кривої та фігури

Отже,

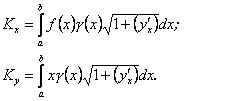(10.15)

Якщо центр ваги має координати ,

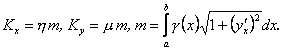
Звідси

(10.16)

Розглянемо тепер питання про знаходження центра ваги плоскої фігури, густина маси якої

Рис.10.11

. Якщо центр ваги фігури (рис. 10.11) знаходиться в точці , а маса фігури , то згідно з формулами (10.16) , для знаходження і потрібно знати статичні моменти і масу фігури. Виділимо на осі елемент і побудуємо смужку, паралельну осі . Її довжина дорівнює Оскільки густина є функцією лише , то по всій довжині смужки густину можна вважати сталою, саму смужку – прямокутником (бо – нескінченно мала величина, а тому центр ваги смужки знаходитиметься в точці з координатами ). Маса смужки . Отже,

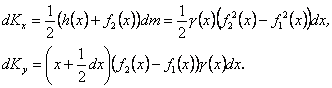
Знехтувавши нескінченно малою вищого порядку, одержимо Остаточно маємо

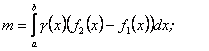(10.17) 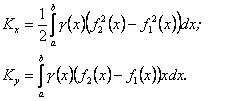(10.18)

Тепер, користуючись формулами (10.16), легко записати координати центра ваги фігури. Можна знайти і статичні моменти деяких тіл, якщо вдасться виразити густину у функції однієї змінної. Із формул (10.15) і (10.16) при , одержимо 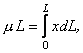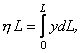де – довжина дуги,

Помноживши останні дві рівності на , матимемо

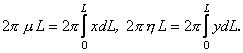
У правій частині цих формул маємо величину поверхні обертання кривої навколо осі, що її перетинає, а в лівій – добуток довжини дуги на довжину кола, описаного з центром ваги кривої, тобто (твердження відоме як перша теорема Гюльдіна). Ця теорема дозволяє знайти площу поверхні обертання кривої, центр ваги якої відомий, навколо осі, що її не перетинає. Наприклад, коло радіуса , обертаючись навколо осі, що знаходиться в площині кола на відстані від центра кола, утворює поверхню, яка називається тором. Центром ваги кола є його центр. Отже, , а довжина кола, описаного центром ваги . Отже, поверхня тора

Розглядаючи формули (10.16) і (10.18), аналогічно одержимо при

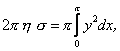
де - площа фігури, що обертається навколо осі, яка її не перетинає, а 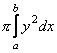- об’єм тіла обертання, тобто остання рівність може бути записана як (друга теорема Гюльдіна).

Для прикладу розглянемо паралелограм зі сторонами і кутом між ними. Нехай вісь обертання походить через вершину паралелограма перпендикулярно до сторони . Легко перевірити , що об’єм тіла обертання