Сторінка
6

Поняття множини. Змінні та постійні величини

Функція означена для всіх значень , крім . Множина значень: .

Обернені тригонометричні функції (рис.5.11, 5.12, 5.13, 5.14).

- нескінченнозначна функція, обернена для функції . Область означення: ; область зміни . Якщо кожному значенню покласти у відповідність значення нескінченнозначної функції , що задовольняє умовам , одержимо однозначну функцію, яку будемо позначати і називати головним значенням функції .

Функція - нескінченнозначна, обернена для функції . Область означення: ; область зміни: . Якщо кожному значенню , покласти у відповідність значення нескінченнозначної функції , що задовольняє умовам , одержимо однозначно функцію, яку будемо позначати і називати головним значенням функції .

Функції і - нескінченнозначні, обернені відповідно для функцій і . Області означення: ; області зміни: , крім відповідно

і .

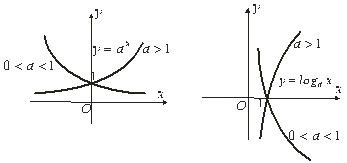
Рис.5.3 Рис.5.4

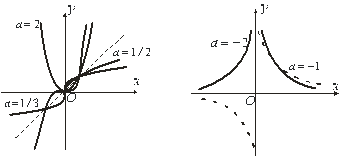
Рис.5.5 Рис.5.6

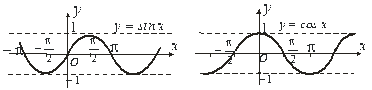
Рис.5.7 Рис.5.8

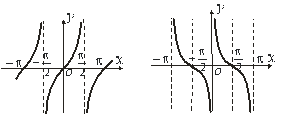
Рис.5.9 Рис.5.10

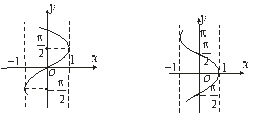
Рис.5.11 Рис.5.12

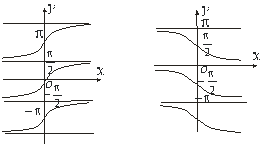
Рис.5.13 Рис.5.14

Якщо кожному значенню , , поставити у відповідність значення функції , що задовольняють нерівностям , то одержимо функцію, яку назвемо головним значенням багатозначної функції і будемо позначати .

Окремі класи функцій.

Нехай функцію задано на деякому проміжку

Монотонні функції. Якщо для кожної пари точок при виконується нерівності:

1) то функція називається зростаючою на проміжку

2) то функція називається неспадною на проміжку

3) то функція називається спадною на проміжку