Сторінка
5

Монотонність функції, необхідні і достатні умови. Eкстремум функції однієї та декількох змінних

Точок, в яких похідна не існує, немає.

Обчислимо значення функції в точках (ці точки належать відрізку ), а також на кінцях відрізка, тобто в точках . Маємо

Отже, найбільше значення становить , найменше -

Щоб знайти найбільше (найменше) значення функції замкненій області , потрібно знайти значення функції у всіх критичних точках і порівняти їх з найбільшими (найменшими) значеннями функції на границях області: найбільше і найменше із цих значень і буде найбільшим і найменшим значенням функції в даній області.

Приклад. Знайти найбільше і найменше значення функції в трикутнику (рис. 6.14), обмеженому прямими .

Р о з в ’ я з о к.

Знайдемо критичні точки функції:

;

;

Оскільки в даній області , то

У критичній точці функція приймає значення

.

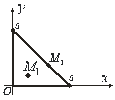
Рис.6.12

Дослідимо поведінку функції на границях області.

На прямих і . На прямій ця функція є функцією однієї змінної , оскільки ;

.

Знайдемо найбільше і найменше значення функції на відрізку :

Критична точка . В цій точці . На кінцях відрізка . Отже, функція досягає найбільшого значення в точці , а найменшого – в точці . Найбільше значення , найменше значення .

Зауваження. До знаходження відповідно найбільшого чи найменшого значення певної функції зводиться цілий ряд практичних задач.