Сторінка
2

Монотонність функції, необхідні і достатні умови. Eкстремум функції однієї та декількох змінних

Обмежимося розглядом функцій, диференційованих скрізь, крім, можливо, скінченого числа точок, в їх областях визначення і які мають не більше скінченого числа точок стаціонарності. Якщо функція розглянутого класу, то доводиться, що її інтервали монотонності розділяються або точками стаціонарності , або точками, в яких похідна функції не існує. Але ж не кожна така точка буде розділяти інтервали монотонності (рис. 6.11).

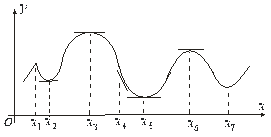
Рис.6.11

Сформулюємо правила дослідження функцій на зростання і спадання.

10.Знаходимо точки із області означення функції, в яких похідна функції дорівнює нулю або не існує. Ці точки називають критичними для функції за першою похідною.

Критичні точки розбивають область означення функції на інтервали, на кожному із яких похідна зберігає знак.

20. Досліджуємо знак на кожному із цих інтервалів.

Якщо на інтервалі , то це інтервал зростання, якщо , інтервал спадання.

Приклад.

Знайти інтервал зростання і спадання функції.

Р о з в ’ я з о к. Обчислимо похідну

.

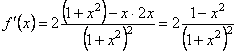Знайдемо точки, в яких . Це точки, в яких . Розв’яжемо цю нерівність:

.

Отже, в інтервалі функція зростає; в інтервалах

функція спадає.

1.2. Екстремуми функцій

Нехай функція визначена в деякій області і точка внутрішньою точкою

області .

Означення. Функція в точці має максимум, якщо для всіх точок деякого околу цієї точки виконується нерівність

. (6.85)

Означення. Функція в точці має мінімум, якщо для всіх точок деякого околу цієї точки виконується нерівність

. (6.86)

Максимуми і мінімуми функції називаються її екстремумами.

Необхідні умови існування екстремуму.

Теорема.1. Якщо диференційована функція має в точці екстремум, то .

Д о в е д е н н я. Нехай, наприклад, функція має в точці максимум. Тоді при достатньо малому , а тому

Переходячи до границі при , одержимо:

Згідно з умовою - диференційована функція в точці . Тому одержані границі дорівнюють . Таким чином, маємо і , отже .

Теорема 2. У точці екстремуму функції кількох змінних кожна її частинна похідна першого порядку або дорівнює нулю, або не існує.

Д о в е д е н н я. Нехай функція в точці має максимум – для конкретності. Зафіксуємо значення всіх змінних, крім однієї, наприклад , поклавши їх рівними між собою: .

Тоді функція стає функцією однієї змінної :

.

За умовою теореми функція має максимум, тобто,

Остання нерівність означає, що функція як функція однієї змінної в точці має максимум. На основі вище доведеної теореми виводимо, що в точці похідна дорівнює нулю або не існує. Аналогічно доведемо, що і всі інші частинні похідні першого порядку в точці дорівнюють нулю або не існують.

Наслідок. В точці екстремуму диференційованої функції виконуються рівності