Сторінка
1

Похідна за напрямком і градієнт функції, основні властивості

План

• Похідна за напрямком
• Градієнт функції
• Основні властивості

1. Похідна функції за напрямком і градієнт

Нехай - функція, означена в області . Розглянемо деяку точку і деякий напрямок , визначений напрямними косинусами і (тобто і - косинуси кутів, утворених вектором з додатними напрямками осей координат і ). При переміщенні в заданому напрямку (рис.7.10) точки в точку функція одержує приріст

, (7.46)

який називається приростом функції в заданому напрямку .

Якщо є величина переміщення точки , то із прямокутного трикутника одержуємо , , отже,

. (7.47)

Означення. Похідною функції в заданому напряму називається границя відношення приросту функції в цьому напрямку до величини переміщення при умові, що останнє прямує до нуля, тобто

. (7.48)

З цієї точки зору похідні і можна розглядати як похідні функції в додатних напрямках осей координат і . Похідна визначає швидкість зміни функції в напрямку .

Виведемо формулу для похідної , вважаючи, що функція диференційована. Із означення диференціала функції випливає, що приріст функції відрізняється від диференціала функції на вищий порядок малості відносно приросту незалежних змінних. Тому

,

де і при і . Звідси в силу співвідношень (7.47) одержуємо

.

Отже,

.

Переходячи до границі в останній формулі при ,тобто при і , одержимо формулу для похідної функції в заданому напрямку:

. (7.49)

Приклад. Обчислити в точці похідну функції в напрямку, що складає кут з віссю .

Р о з в ’ я з о к.

.

Зауваження. Для функції її похідна в напрямку дорівнює

(7.50)

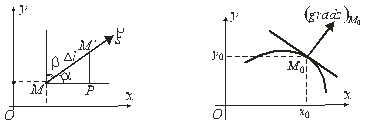
Рис.7.10 Рис.7.11

При вивчені поведінки функції в даній точці площини аргументів найбільшу зацікавленість являє питання про напрямок найвищого зростання в цій точці. Задача розв’язується за допомогою вектора, який називається градієнтом функції .