Сторінка
3

Монотонність функції, необхідні і достатні умови. Eкстремум функції однієї та декількох змінних

(6.87)

Означення. Точки, в яких частинні похідні першого порядку деякі функції дорівнюють нулю або не існують, називаються критичними точками.

Із доведеної теореми витікає, що екстремум функції кількох змінних може досягатись лише в критичних точках.

Для диференційованої функції двох змінних критичні точки знаходяться із системи рівнянь

(6.88)

Приклад.

Знайти критичні точки функції

Р о з в ’ я з о к. Прирівнюючи до нуля частинні похідні даної функції, одержуємо систему рівнянь для знаходження координат критичних точок:

Функція має чотири критичні точки:

.

Достатні умови існування екстремуму.

Теорема. Нехай є критична точка функції , яка в цій точці є неперервною, і нехай існує окіл точки , в якому має похідну , крім, можливо, точка . Тоді:

1) якщо в інтервалі похідна , а в інтервалі похідна , то є точкою максимуму функції ;

2) якщо в інтервалі , а в інтервалі то є точкою мінімуму функції ;

3) якщо в обох інтервалах і похідна має той самий знак ( набуває або тільки додатних, або тільки від’ємних значень), то не є екстремальною точкою функції .

Перше правило дослідження функції на екстремум. Щоб дослідити функцію на екстремум, треба:

1) знайти стаціонарні точки даної функції (для цього слід розв’язати рівняння , причому з його коренів вибрати тільки дійсні і ті, які є внутрішніми точками області існування функції).

2) знайти точки, в яких похідна не існує (функціяв цих точках існує);

3) у кожній критичній точці перевірити зміну знака похідної першого порядку.

Приклади.

1. Дослідити на екстремум функцію.

Р о з в ’ я з о к. 1). Знаходимо

.

Розв’язуємо рівняння :

Звідси визначаємо стаціонарні точки

2). Точок, в яких похідна не існує, немає. Отже, стаціонарні точки є єдиними критичними точками заданої функції.

3). Розглянемо інтервали

.

Для визначення знака похідної обчислимо останню в довільних точках, які належать даним інтервалам. Візьмемо, наприклад, такі точки: .

Тоді:

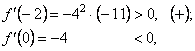
Отже, при переході через точку похідна змінює знак з “+” на “-” ; у цій точці функція має екстремум який дорівнює при переході через точку похідна змінює знак “-” на “+”; у цій точці функція має мінімум, який дорівнює ; при переході через критичну точку похідна знак не змінює; точка не є екстремальною для заданої функції

Теорема. Нехай точка є стаціонарною для функції і нехай в цій точці існує похідна другого порядку , яка не

дорівнює нулю, . Тоді, якщо то є точкою

мінімуму; якщо , - точкою максимуму функції .

Друге правило дослідження функції на екстремум. Щоб дослідити функцію на екстремум, треба знайти:

1) стаціонарні точки заданої функції

2) похідну другого порядку в стаціонарній точці.

3) якщо то в цій точці функція має максимум, якщо мінімум.

Приклад. Користуючись другим правилом, дослідити функцію на екстремум.

Р о з в ’ я з о к. Знаходимо похідну . Прирівнюємо її до нуля і розв’язуємо рівняння