Сторінка
25
Для перевірки наявності автокореляції залишків найчастіше застосовується критерій Дарбіна-Уотсона ![]() :
:
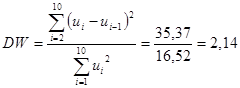 .
.
Оскільки критерій ![]() більше двох, то можна говорити про існування від’ємної автокореляції.
більше двох, то можна говорити про існування від’ємної автокореляції.
Фактичні значення критерію ![]() порівняємо з критичними (табличними) для рівного числа спостережень
порівняємо з критичними (табличними) для рівного числа спостережень ![]() і числа незалежних змінних
і числа незалежних змінних ![]() . Табличні значення мають нижню межу
. Табличні значення мають нижню межу ![]() і верхню межу
і верхню межу ![]() .
.
Оскільки ![]() , то приймається гіпотеза про відсутність автокореляції.
, то приймається гіпотеза про відсутність автокореляції.
Для виявлення автокореляції залишків використовується також критерій фон-Неймана:
![]() .
.
Фактичне значення критерію фон-Неймана порівняємо з табличним. При рівні значущості ![]() і заданому числу спостережень
і заданому числу спостережень ![]()
![]() .
.
Так як ![]() , автокореляції залишків відсутня.
, автокореляції залишків відсутня.
Крок 3. Формування матриці коваріації залишків.
Сформуємо матриці ![]() і
і ![]() . Для цього необхідно знайти циклічний коефіцієнт автокореляції
. Для цього необхідно знайти циклічний коефіцієнт автокореляції ![]() :
:
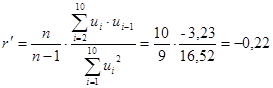 .
.
Параметр ![]() має зміщення. Тому, використовуючи його для формування матриці
має зміщення. Тому, використовуючи його для формування матриці ![]() , скоригуємо на величину зміщення:
, скоригуємо на величину зміщення:
![]() ,
,
або ![]() .
.
Матриця ![]() матиме вигляд:
матиме вигляд:
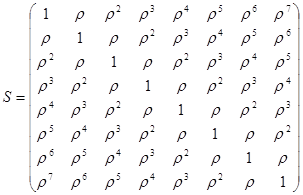 ,
,
де ![]() .
.
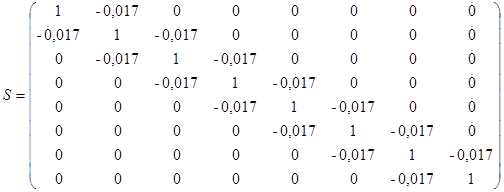 .
.
Розрахуємо залишкову дисперсію:
![]() .
.
Тоді матриця коваріацій ![]() , тобто:
, тобто:
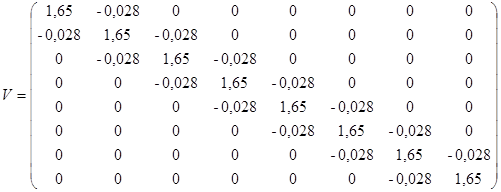 .
.
Крок 4. Виконаємо обертання матриці ![]() :
:
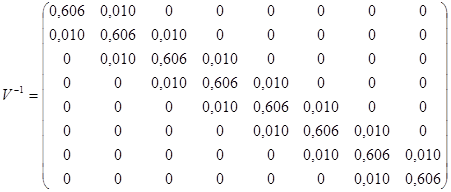 .
.
Крок 5. Визначимо параметри ![]() і
і ![]() на основі співвідношення:
на основі співвідношення:
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
; ![]() .
.
Отже, рівняння регресії запишеться: ![]() .
.
Тепер знайдемо розрахункові значення ![]() і визначимо залишки
і визначимо залишки ![]() .
.
Таблиця 3.7.
| Рік |
|
|
|
|
|
|
|
| 1. | 21 | 21,51 | -0,51 | 0,26 | – | – | – |
| 2. | 23,4 | 23,58 | -0,18 | 0,03 | 0,33 | 0,11 | 0,09 |
| 3. | 25,6 | 27,35 | -1,75 | 3,06 | -1,57 | 2,46 | 0,32 |
| 4. | 24,4 | 23,96 | 0,44 | 0,20 | 2,19 | 4,80 | -0,77 |
| 5. | 29,8 | 27,91 | 1,89 | 3,55 | 1,44 | 2,08 | 0,83 |
| 6. | 26,2 | 27,54 | -1,34 | 1,79 | -3,22 | 10,39 | -2,52 |
| 7. | 28,6 | 27,35 | 1,25 | 1,56 | 2,59 | 6,70 | -1,67 |
| 8. | 29,4 | 28,29 | 1,11 | 1,23 | -0,14 | 0,02 | 1,39 |
| 9. | 30,6 | 29,61 | 0,99 | 0,98 | -0,12 | 0,01 | 1,10 |
| 10. | 28,4 | 30,36 | -1,96 | 3,86 | -2,95 | 8,72 | -1,94 |
| 16,52 | 35,30 | -3,19 |
