Сторінка
3

Задача Коші. Лінійні диференціальні рівняння із сталими коефіцієнтами. Загальний та частинний розв’язки

(7)

Об’єднаємо випадки а).-в).: якщо права частина рівняння (5) має вигляд (6), то частинний розв’язок цього рівняння треба шукати у вигляді

де - многочлен з невизначеними коефіцієнтами того самого степеня, що й многочлен - число коренів характеристичного рівняння, які дорівнюють . Якщо не є коренем характеристичного рівняння, то приймаємо r=0.

ІІ. Нехай права частина в рівнянні (5) має вигляд

, (8)

де Pn(x) – многочлен степеня п, Rm(x) - многочлен степеня m; - дійсні числа. (Функція (6) є окремим випадком функції (98) і утворюється з неї при ).

Частинний розв’язок рівняння (5) треба шукати у вигляді

, (9)

де Rs(x) ma Ls(x) – многочлени степеня s з невизначеними коефіцієнтами; s – найвищій степінь многочленів Rs(x) ma Ls(x), тобто s=max(n;m); r – число коренів характеристичного рівняння, які дорівнюють

зокрема, якщо права частина рівняння (5) має вигляд

(10)

де А, В – невідомі дійсні числа, то частинний розв’язок цього рівняння треба шукати у вигляді

(11)

де а , b – невідомі коефіцієнти; r –число коренів характеристичного рівняння (7), які дорівнюють .

Приклад.

Розв’язати рівняння

Характеристичне рівняння має корені тому загальний розв’язок однорідного рівняння має вигляд . Оскільки правою частиною даного рівняння є функція виду , причому , то за формулою (6) частинний розв’язок шукаємо у вигляді тобто , де А і В – невідомі коефіцієнти. Знайшовши похідні і підставивши їх у рівняння дістанемо

-2В+А+Вх=2х+3.

Порівнюючи коефіцієнти при однакових степенях, дістанемо систему рівнянь

звідки В=2, А=7. Отже, частинний розв’язок даного рівняння має вигляд , тому

шуканий загальний розв’язок.

Лінійні диференціальні рівняння п-го порядку.

Застосовуємо методи знаходження розв’язків диференціальних рівнянь другого порядку до рівнянь вищих порядків. Не зупиняючись детально на теорії, сформулюємо необхідні твердження і розглянемо приклади.

Нехай маємо лінійне диференціальне рівняння п-го порядку

(12)

де а1, а2, .,ап – сталі дійсні числа.

Характеристичним для рівняння (12) називається алгебраїчне рівняння п-го степеня виду

(13)

де k – невідоме дійсне чи комплексне число.

Як відомо рівняння (13) має п коренів. Позначимо ці корені через

Теорема. Кожному простому кореню k рівняння (13) відповідає частинний розв’язок рівняння (12), а кожному кореню k кратності m>1 відповідає т частинних розв’язків виду

Кожній парі простих комплексно-спряжених коренів рівняння (13) відповідає два частинних розв’язки рівняння (12), а кожній парі комплексно-спряжених коренів кратності р>1 відповідає 2р частинних розв’язків виду

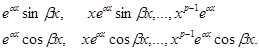
Загальна сума кратностей всіх коренів рівняння (13) дорівнює п, тому кількість всіх частинних розв’язків рівняння (12), складених згідно з цією теоремою, дорівнює п , тобто збігається з порядком рівняння (12). Позначимо ці частинні розв’язки через у1, у2, ., уп. . Можна показати, що знайденні частинні розв’язки є лінійно незалежними, і загальний розв’язок рівняння (12) знаходиться за формулою