Сторінка
4

Задача Коші. Лінійні диференціальні рівняння із сталими коефіцієнтами. Загальний та частинний розв’язки

(14)

Нехай тепер задано неоднорідне рівняння п- го порядку

(15)

Де - сталі дійсні числа, - неперервна на деякому проміжку функція.

Як і для рівнянь другого порядку, загальним розв’язком рівняння (15) є функція:

де - загальний розв’язок відповідного однорідного рівняння (12), а у*(х) – частинний розв’язок рівняння (15).

Побудову загального розв’язку рівняння (12) з’ясовано. Проаналізуємо знаходження частинного розв’язку у*(х). Якщо права частина f(x) рівняння (15) є функцією спеціального виду (8), то частинний розв’язок цього рівняння треба шукати за формулою (9). Якщо права частина f(x) не є функцією виду (8), то для знаходження у*(х) застосовують метод варіації довільних сталих. Стосовно рівняння (15) суть цього методу така.

Нехай функція (14) є загальним розв’язком відповідного однорідного рівняння (12). Знаходимо частинний розв’язок рівняння (15) за тією ж формулою (14), вважаючи, що величини С1, С2, ., Сп – функції від х, тобто покладемо

де С1(х), С2(х), ., Сп(х) – невідомі функції.

Складемо систему рівнянь

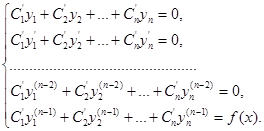
Розв’язуючи цю систему, знаходимо похідні і=1,2, .,п, а потім інтегруванням і самі функції Сі(х). Якщо взяти всі сталі інтегрування рівними нулю і підставити функції Сі(х) в рівність (16), то матимемо частинний розв’язок рівняння (15); якщо у рівність (16) підставити функції де - довільні сталі, то зразу дістанемо загальний розв’язок.

Приклад.

Розв’язати рівняння

Характеристичне рівняння має корені k1=k2=ks=0, k4=2i, ks=-2i.згідно з теоремою маємо частинні розв’язки: у1=1, у2=х, у3=х2, у4=cos2x . y5=sin2x. Загальний розв’язок даного рівняння знаходимо з а формулою (14):

V. Контрольні питання:

1. Як знаходять характеристичне рівняння диференціального рівняння.

2. Які три випадки можливі, якщо позначити корені характеристичного рівняння через k1 і k2.

3. Сформулювати теорему для диференціальних рівнянь n-порядку.

4. Сформулювати теорему Коші про існування та єдність розв’язку для рівняння y”=f(x, y, y,).

VІ. Література:

1. 1.Барковський В.В. Барковська Н.В. ”Математика для економістів”. 1. Вища математика. – К.: Національна академія управління, 1997 р. – 397 ст. , ст. 10-12, 19-20.

2. 2.Дубовик В.П., Юрик І.І. Вища математика: Навч. посібник. – К.: А.С.К., 2001.– 648 с.