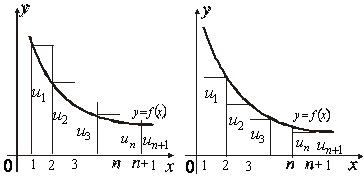Сторінка
3

Достатні ознаки збіжності рядів з додатніми членами: ознаки порівняння, Даламбера, радикальна та інтегральна ознаки Коші

звідки випливає, що

або

Розглянемо тепер два ряди:

,

.

Другий ряд збігається, оскільки його члени утворюють геометричну прогресію. Члени першого ряду, починаючи з , менші за члени другого ряду, а тому він за ознакою порівняння збігається.

2) Нехай Тоді, починаючи з деякого номера , будемо мати

або

Але, якщо всі члени даного ряду, починаючи з деякого , більші за одиницю, то ряд розбігається, оскільки його загальний член не прямує до нуля.

Зауваження. Як і в ознаці Даламбера, випадок вимагає додаткового дослідження. Серед таких рядів можуть зустрітися як збіжні, так і розбіжні.

Приклад. Дослідити збіжність ряду

.

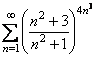Р о з в ‘ я з о к. Використаємо радикальну ознаку Коші:

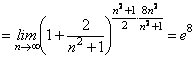>1 – ряд розбігається.

13.6. Інтегральна ознака Коші

Розглянемо ще одну ознаку, яка відрізняється по формі від всіх попередніх.

Нехай ряд має форму

, (13.11)

і є значення при деякої функції , визначеної для . Припустимо, що ця функція неперервна, додатна і монотонно спадна.

Теорема. Нехай члени ряду (13.11) додатні і не спадають, тобто

(13.12)

і нехай така неперервна неспадна функція, що

(13.13)

Тоді :

1) якщо невласний інтеграл 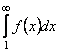збігається, то збігається і ряд (13.11);

2) якщо невласний інтеграл 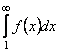розбігається, то розбігається і ряд (13.11).

Д о в е д е н н я. Зобразимо члени ряду геометрично, відкладаючи на осі абсцис номера членів ряду, а на осі ординат – відповідні значення членів ряду . Побудуємо на цьому ж рисунку графік неперервної функції , що задовольняє умові (13.13). Ясно, що ця функція буде проходити через точки (рис. 13.1).

Рис.13.1 Рис.13.2

Зауважимо, що площа го прямокутника дорівнює , а сума площ побудованих прямокутників дорівнює частинній сумі ряду З іншого боку, ступенева фігура, утворена цими прямокутниками, містить область, що обмежена кривою і прямими ; площа цієї області дорівнює 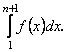Отже,

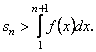(13.14)

На рис.13.2 перший (зліва) із побудованих прямокутників має висоту , а тому його площа буде Площа другого прямокутника і т.д. Площа останнього із побудованих прямокутників буде

Отже, сума площ всіх побудованих прямокутників дорівнює

З іншого боку, як легко помітити, ступенева фігура, утворена цими прямокутниками, міститься всередині криволінійної трапеції, обмеженої кривою і прямими

Площа цієї криволінійної трапеції дорівнює 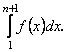Тому

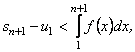
звідки

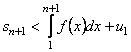. (13.15)

Розглянемо тепер обидва випадки.

1). Нехай невласний інтеграл 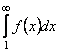збігається. Оскільки

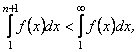
то в силу нерівності (1.15) будемо мати

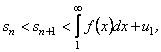
тобто частинна сума ряду, яка є монотонно зростаючою (члени ряду додатні) , залишається обмеженою. Значить, при має скінчену границю , тобто ряд збігається.

2). Нехай невласний інтеграл 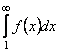розбігається, тобто 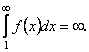Це значить, що 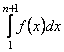необмежено зростає при зростанні Але, в силу нерівності (13.14), також необмежено зростає при зростанні , тобто ряд розбігається.