Сторінка
3

Послідовності випадкових величин. Граничні теореми

Наслідок. Інтегральна гранична теорема Муавра- Лапласа.

Проводяться незалежні випробовування. При кожному випробовуванні з’являється успіх з ймовірністю р ( 0або невдача з ймовірністю q. Нехайчисло успіхів при n- випробуваннях. Тоді при а

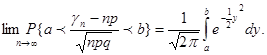
Для доведення достатньо ввести випадкові величини

якщо в к-тому випробовуванні був успіх;

o, якщо в к-тому випрбовуванні була невдача.

Тоді ; M; D і залишається застосувати попередню теорему.

Задача 1. Ймовірність влучення мішені при одному пострілі дорівнює 0,8. Знайти ймовірність того, що при 100 пострілах в мішень буде влучено рівно 75 разів. (Скористатися локальною теоремою Лапласа при m=75, , ).

Задача 2. Ймовірність появи події А в кожному випробовуванні дорівнює . Скориставшись нерівністю Чебишова, оцінити ймовірність того, що число появ події А змінюється в межах від 40 до 60, якщо буде проведено 100 незалежних випробовувань.

Розв’язок. Знайдемо математичне сподівання та дисперсію дискретної випадкової величини - числа появ події А в100 незалежних випробовуваннях.

; =25. Знайдемо максимальну різницю між

заданим числом появ події та математичним сподіванням М=50: =60-50=10.

Скористаємося нерівністю Чебишова в формі

.

Підставляючи М=50, D=25, =10, одержимо

Задача 3. Ймовірність деякої події А в кожному випробовуванні із серії n незалежних випробувань дорівнює р=. Використовуючи нерівність Чебишева, оцінити ймовірність того, що частота цієї події відхилиться від її ймовірності по абсолютній

60

величині не більше чим на 0, 01, якщо буде проведено n=9000 випробувань ( Відповідь 0, 75 ).

Задача 4. Послідовність незалежних випадкових величин 1, 2 ,…, n,… задана законом розподілу

n - 0

p .

Чи можна застосувати до заданної послідовності теорему Чебишева?

Розв’язок. Для того, щоб до заданої послідовності випадкових величин була застосована теорема Чебишова, достатньо, щоб ці величини були попарно незалежні, мали скінчене математичне сподівання та рівномірно обмежені дисперсії.

Оскільки випадкові величини незалежні, то вони і подавно незалежні, тобто перша вимога теореми Чебишова виконується.

Перевіримо чи виконується вимога скінченості математичних сподівань:

Таким чином, кожна випадкова величина має скінчене ( рівне нулю ) математичне сподівання , тобто друга умова теореми виконана.

Перевіримо, чи виконується вимога рівномірної обмеженості дисперсії. Запишемо закон розподілу :

0

p

Звідси випливає, що дисперсії заданих випадкових величин рівномірно обмежені числом . Таким чином, до заданної послідовності випадкових величини можна застосувати теорему Чебишева.

Задача 5. Випадкові величини 1, 2 ,…, n,… - незалежні і рівномірно розподілені на відрізку [a, b]. Чи можна застосувати до цієї послідовності закон великих чисел ?