Сторінка
2

Послідовності випадкових величин. Граничні теореми

Теорема Хінчина. Нехай { }- послідовність незалежних одинаково розподілених величин, які мають скінчене математичне сподівання М=а. Тоді для кожного

.

Теорема Маркова. Нехай випадкові величини1, 2 ,…, n як завгодно залежні. Для виконання ( * ) достатньо, щоб

при .

Теорема Бернуллі. Нехай маємо послідовність випробовувань, в кожному з яких можуть бути два наслідки- успіх У ( з ймовірністю р ) або невдача Н ( з ймовірністю q=1-p) незалежно від наслідків інших випробувань. Утворимо послідовність випадкових величин наступним чином. Нехай к =1, якщо в к-тому випробовуванні був успіхк =0, якщо в к-тому випробовуванні наступила невдача. Тоді { }- є послідовність незалежних одинаково розподілених випадкових величин Mк=p, Dк=pq. Випадкова величина представляє собою частоту появи успіху в перших n випрбуваннях. Оскільки для послідовності { }-виконані умови теореми Чебишова, то із теореми Чебишова одержуємо наступне твердження.

Теорема Бернуллі. Для довільного Р{при n.

Зміст цього твердження полягає в тому, що ведене нами визначення ймовірності відповідає інтуїтивному розумінню ймовірності як границі частоти.

58

3.2 Посилений закон великих чисел.

Послідовність випадкових величин { ,n}- збігається з ймовірністю 1 до величини , якщо ймовірність всіх тих точок , для яких не існує,

або , дорівнює нулю, тобто якщо Р{{.

Розглянемо послідовність випадкових величин k з скінченими математичними сподіваннями. Теореми, які стверджують, що різниця збігається з ймовірністю 1 до нуля, називається посиленим законом великих чисел. Нижче приводиться дві теореми про посилений закон великих чисел, обидві вони доведені.

А. М. Колмагоровим.

Теорема 1. Нехай n – послідовність незалежних випадкових величин, для яких М, Dвизначені. Якщо

, то Р {-)=0}=1.

Наслідок ( теорема Бореля ). Припустимо, що розглядається послідовність незалежних випробувань, в кожному з яких з’являеться успіх У з ймовірністю р або невдача Н з ймовірністью q=1-p. Нехай - число успіхів при n випробуваннях. Тоді Р{ }=1.

Це випливає з того, що =, де k- послідовність незалежних випадкових величин введених при доведенні теореми Бернуллі.

Теорема 2. Нехай- послідовність незалежних одинаково розподілених величин з скінченим математичним сподіванням М=а. Тоді

Р {=а}=1.

3.3 Центральна гранична теорема.

Теорема. Нехай 1, 2 ,…, n,…- послідовність незалежних випадкових величин з скінченною дисперсією (і

.

Тоді при nдля довільного x

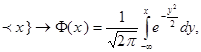
59

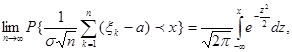( де = ).

Це один з самих видатних результатів теорії ймовірностей: при широких припущеннях відносно суми великої кількості незалежних малих випадкових доданків має місце розподіл, який близький до нормального ( гаусівського).