Сторінка
1

Інтерполяція

План

• Інтерполяція
• Інтерполяційна формула Лагранжа
• Інтерполяційна формула Ньютона

13.16. Інтерполювання функцій

Нехай відомі числові значення деякої величини , які відповідають числовим значенням величини /вузли інтерполювання /. Вважаючи функцією від , складемо таблицю із цих чисел:

Такі таблиці виникають на практиці в результаті дослідів, які проводяться над величиною ; але їх складають і для аналітично заданих функцій : таблиці квадратів та кубів чисел, таблиці логарифмів, таблиці тригонометричних функцій і т.п.

Часто виникає потреба в ущільненні таблиць, тобто в обчисленні проміжних значень , відсутніх в таблиці, задовольнившись при цьому лише наявним запасом табличних значень цієї величини . Також буває потрібним знайти на базі таблиці аналітичний вираз деякої функції , яка набувала б табличних значень за табличних значень . Звичайно, за беруть многочлен степеня , що має таку властивість (інтерполюючий многочлен).

Ознайомимося з деякими методами інтерполювання.

13.16.1. Інтерполяційна формула Лагранжа

Інтерполяційний многочлен запишемо у вигляді:

Для знаходження невизначених коефіцієнтів будемо покладати в цій рівності по черзі вимагаючи при цьому, щоб

Тоді одержуємо

Підставивши знайдені значення коефіцієнтів у вираз інтерполяційного многочлена, одержимо інтерполяційну формулу Лагранжа:

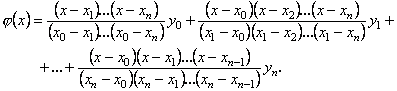
Поклавши в цю формулу , що дорівнює потрібному нам проміжному (нетабличному) значенню, одержуємо відповідне проміжне (нетабличне) значення . За табличних значень маємо відповідні табличні значення .

13.16.2. Інтерполяційна формула Ньютона

У випадку, коли вузли інтерполювання утворюють арифметичну прогресію (рівновіддалені)

( - крок інтерполювання), користуються інтерполяційною формулою, яка використовує скінченні різниці функції .

Скінченою різницею першого порядку величини називається різниця між двома послідовними її табличними значеннями:

Скінченою різницею другого порядку величини називається різниця між двома послідовними різницями першого порядку:

Аналогічно визначаються і скінченні різниці вищих порядків.

Із означень одержуємо:

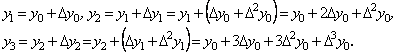
Можна показати методом математичної індукції, що і в загальному випадку коефіцієнти виразу є біноміальними, а весь вираз нагадує розгорнутий -ий степінь суми. Тому