Сторінка
2

Обчислення подвійного інтеграла в декартових і полярних координатах

Згідно з формулою (11.16) об’єм усього тіла дорівнюватиме інтегралу від , якщо .

Рис.11.6

Замінюючи у формулі (11.16) її виразом (11.17), дістаємо

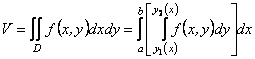
або в зручнішій формі

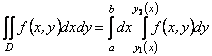. (11.18)

Міняючи і місцями, можна вивести й формулу:

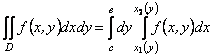. (11.19)

З (11.18) і (11.19) бачимо, що значення повторного інтеграла (що стоїть у правій частині рівності (11.18) або (11.19) ) не залежить від порядку інтегрування за різними аргументами:

.

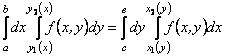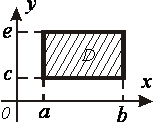
Формули (11.18) і (11.19) показують, що обчислення подвійного інтеграла зводиться до послідовного обчислення двох звичайних визначених інтегралів; потрібно тільки пам’ятати, що у внутрішньому інтегралі одна зі змінних при інтегруванні вважається сталою величиною. Формули (11.18) і (11.19) зведення подвійного інтеграла до повторного набирають простого вигляду, коли область буде прямокутником зі сторонами, паралельними осям координат (рис. 11.6). В цьому разі сталими стають межі інтегрування не тільки в зовнішньому, а й у внутрішньому інтегралі:

.

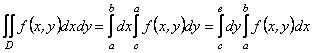Отже, подвійний інтеграл можна обчислювати за такою схемою:

1. Спроектувати область на вісь (знайти точки і ).

2. Провести пряму, паралельну осі , яка перетинає межу області в точках входу в область і виходу з неї. Записати рівняння цих меж, тобто рівняння і .

3. Розставити межі інтегрування за змінною і змінною в повторному інтегралі (11.18) і обчислити його.

Зауваження. Якщо область неправильна в напрямі осі , то необхідно таку область розбити прямими , паралельними , на кілька правильних областей.

За аналогічною схемою обчислюється подвійний інтеграл (11.19).

Приклад. Обчислити подвійний інтеграл

,

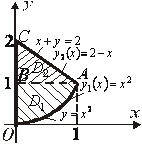
де областьобмежена лініями (рис. 11.7).

Р о з в ’я з о к. В напрямі осі область правильна. Спроектувавши область на вісь маємо: . Крива входу

Рис.11.7

Крива входу описується рівнянням , а лінія виходу - рівнянням . За формулою (11.18) маємо:

.

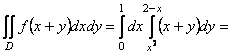
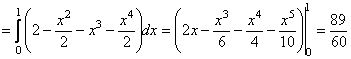Якщо змінити порядок інтегрування, то в напрямі осі область буде неправильною. Таку область потрібно розбити на дві області: і (на рис. 11.7 області відповідає фігура , а області - трикутник ). Тоді:

.

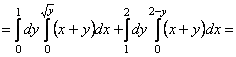
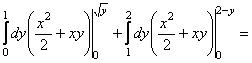
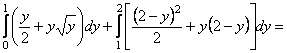
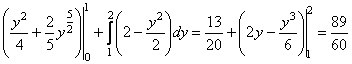2. Обчислення подвійного інтеграла в полярних координатах

Віднесемо площину, в якій задана область , до полярної системи координат . Нехай полюс лежить у початку декартової системи і полярна вісь збігається з віссю . Тоді декартові координати точки визначаються через полярні за формулами .

Область інтегрування розіб’ємо на елементарні області двома системами координатних ліній: (відповідно концентричні кола з центром у полюсі і промені, які виходять із полюса (рис. 11.8)). При цьому елементарними областями будуть криволінійні чотирикутники. Площа області буде: