Сторінка
3

Задачі геометричного і фізичного змісту, що приводить до поняття подвійного інтеграла

яку будемо називати інтегральною сумою Рімана функції що відповідає даному розбиттю.

Якщо існує скінчена границя послідовності інтегральних сум коли максимальний діаметр частинних множин ( ) і вона не залежить від вибору точок в , а також не залежить від способів розбиття області , то ця границя називається кратним інтегралом від функції на (або по ). Отже,

. (11.6)

Зауваження. Чи будемо ми обчислювати границю (11.6) для області , чи для її замикання не має значення, оскільки де кусково-гладка границя області А кусково-гладка границя області має вимірну міру нуль .

2. Властивості подвійних інтегралів. Теорема існування

Будемо надалі вважати області із кусково-гладкими границями.

10. Справедлива рівність

(11.7)

Щоб обчислити інтеграл (11.7), потрібно область розрізати кусково-гладкими поверхнями на частини

що можуть перетинатися хіба що по своїх границях (рис. 11.2), і врахувати, що

Але тоді

За формулою (11.7) у двохвимірному випадку обчислюється площа в трьохвимірному – об’єм В - вимірному випадку формула (11.7) дає - вимірну міру

Нижче ми допускаємо, що для функцій , , , про які буде йти мова, існують інтеграли, що розглядаються.

20. Справедлива рівність

(11.8)

де і константи.

30. Якщо область з кусково-гладкою границею розрізана на вимірні частини і то

(11.9)

40. Якщо

то має місце нерівність

(11.10)

Доведення властивостей 30 і 40 аналогічне доведенням для звичайного означеного інтеграла.

50. Справедлива нерівність

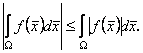(11.11)

Дійсно, враховуючи, що отримаємо в силу (12.8) (при ) і (4.10)

тобто (11.11).

60. Якщо то

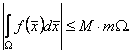(11.12)

константа, а тому в силу нерівності (11.11) маємо:

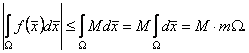
70 . ( Теорема про середнє ). Нехай функція неперервна в замкнутій області яку ми будемо вважати зв’язною 1). Тоді існує точка така , що виконується рівність

(11.13)

Д о в е д е н н я. Оскільки функція неперервна в замкнутій області то вона досягає в цій області свого найменшого та найбільшого значень Тому

Інтегруючи ці нерівності по і використовуючи властивості 10, 40 , одержимо

. (11.14)