Сторінка
4

Інтегрування з допомогою заміни змінної та інтегрування частинами

Обчислимо спочатку перший інтеграл

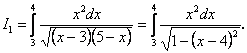
Підстановка зведе інтеграл до вигляду

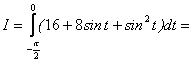
Тут варто зазначити, що підстановка звела невласний інтеграл до інтеграла у звичайному його розумінні.

Аналогічно другий інтеграл

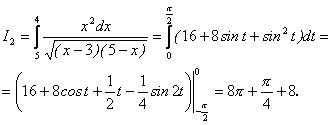
Остаточно одержимо: Заданий інтеграл виявився збіжним.

Ознаки збіжності невласних інтегралів від необмежених функцій.

Тут можна обмежитися розглядом лише невласного інтеграла вигляду 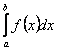, де функція перетворюється в нескінченність лише в точці , бо всякі інші випадки, як це було показано раніше, можуть бути зведені до розглядуваного тут.

Для такого інтеграла є правильними такі твердження (дуже схожі до тих, що розглядалися у процесі вивчення інтегралів з нескінченними границями):

10. Якщо на інтервалі , то інтеграл

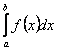збіжний тоді і тільки тоді, коли функція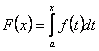

існує і скінчена на інтервалі .

20. Інтеграл 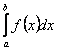тоді і тільки тоді збіжний, коли для всякого знайдеться таке , що 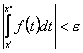, якщо належать відкритому інтервалу .

30. Якщо 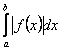збіжний, то збіжним є інтеграл 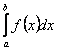.У цьому випадку 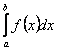називається абсолютно збіжним, а функція - абсолютно інтегрованою.

40. Нехай функція , невласний інтеграл

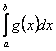збіжний і на інтервалі виконується нерівність . Тоді існує і буде збіжним інтеграл 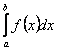. Якщо при цьому і , то із розбіжності інтеграла 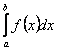випливає розбіжність інтеграла 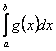(теорема порівняння).

50. За функцію порівняння зручно брати функцію . На інтервалі , якщо , маємо:

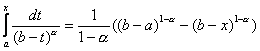
і для

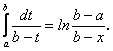
Звідси випливає, що інтеграл (, - дійсне число) збіжний при При цей інтеграл розбіжний.

60. Із п.п. 40 і 50 випливає, що 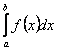збіжний, якщо функція на інтервалі обмежена, а при він розбіжний.

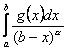Цей результат одержуємо з рівності Справді, оскільки збіжний, то збіжним буде і .

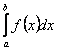На основі твердження п. 60 очевидним стає факт збіжності інтегралів

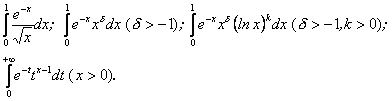
Жоден з цих інтегралів не виражається через елементарні функції в скінченому вигляді.