Сторінка
4

Загальний розв'язок задачі термінального керування і спостереження

У випадку системи спостереження з неперевним аргументом

, . (25)

Стан будемо шукати у вигляді наступної лінійної операції

.

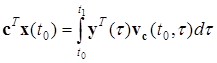Функція представляється як керування в системі

(26)

по переводу її траєкторії з точки в точку .

При розв'язанні задачі термінального керування для систем з неперервним аргументом можливі два випадки.

1) 1) Існує множина розв'язків задачі термінального спостереження для систем із неперевним аргументом.

Необхідна і достатня умова існування множини розв'язків задачі термінального спостереження системою (26) наступне

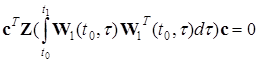, (27)

де - матриця імпульсних перехідних характеристик для системи (26). Якщо на інтервалі виконується умова (27), то існує множина розв'язків задачі термінального спостереження

,

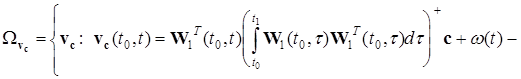
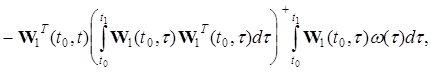
де - інтегровані функції на інтервалі .

Вектор стану системи (25) має вид

,

.

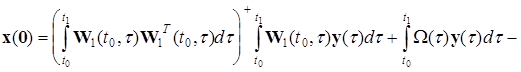
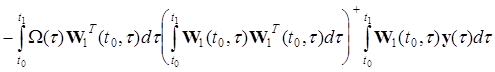Матричні функції інтегровані на інтервалі .

2) Розв'язок задачі термінального спостереження не існує.

У цьому випадку множина псевдорозв'язків задачі термінального спостереження визначається виразом

.

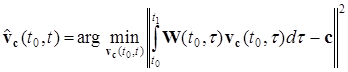Необхідна і достатня умова розв'язку задачі термінального спостереження наступне

.

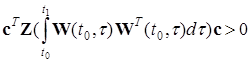Множина псевдорозв'язків задачі термінального спостереження має вид

,

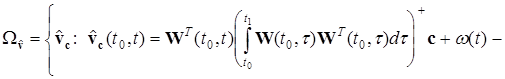
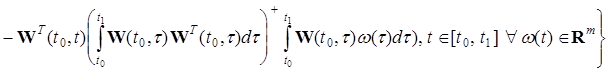Оцінка вектора стану системи (25) представляється такий чином

,

.

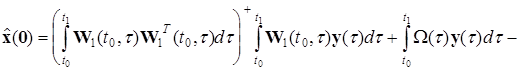
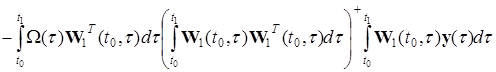Матричні функції інтегровані на інтервалі .