Сторінка
2

Границя та неперервність функцій багатьох змінних

У частковому випадку для функції двох змінних можна розглядати дві повторні границі в точці :

Наприклад, для функції маємо

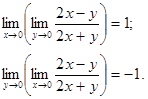
Отже, змінювати порядок граничних переходів загалом не можна.

Скажімо, у попередньому прикладі не існує, але повторні границі існують:

Неперервність функцій двох змінних

Означення. Функція називається неперервною в точці , якщо

Означення. Функція неперервною в області (замкненій чи відкритій), якщо вона неперервна в кожній точці цієї області.

Означення. Функцію , визначену на множині , називають неперервною за множиною в точці , якщо

Означення. Точка називається точкою розриву функції , якщо:

1. функція не визначена в точці ;

2. функція не визначена в точці , проте:

· не існує;

· існує, але не дорівнює

Означення. Точка називається точкою усувного розриву функції , якщо існує, але або не визначена в точці , або

Неперервність складеної (складної) функції двох змінних

Означення. Нехай функція визначена на множині ,а змінні і , у свою чергу, залежать від змінних і : , причому обидві функції та визначені на множині . Якщо для будь-якого існує значення , то говорять, що на множині визначено складену (складну) функцію де ; ,--проміжні, , --незалежні змінні.

Приклад. Функція , де Це складена функція, яка визначена на координатній площині. Її можна записати у вигляді

Теорема 1.6. нехай на множині визначено складену функцію , де і нехай функції неперервні в точці , а функція неперервна в точці , де Тоді складена функція неперервна в точці .

Доведення. За умовою теореми функція неперервна. За означенням неперервності функції в точці візьмемо довільне число , тоді існує , що з нерівності

(5)

випливає нерівність

Аналогічно функції за умовою теореми неперервні, тому існують такі і , що з нерівностей