Сторінка
3

Границя та неперервність функцій багатьох змінних

і

випливають нерівності

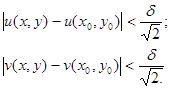(6),(7)

Нехай . Тоді з нерівності

(8)

дістанемо нерівності (6) і (7).

З урахуванням нерівностей (6) і (7) для нерівності (5) запишемо:

.

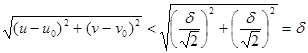Отже, якщо виконується нерівність (8), маємо

,

а це означає, що складена функція неперервна в точці .