Сторінка
2

Властивості степеневих рядів. Неперервність суми. Інтегрування і диференціювання степеневих рядів

Наслідок. Якщо степеневий ряд збігається в інтервалі то його сума представляє собою функцію, що має всередині інтервалу збіжності похідні довільного порядку, кожна з яких є сумою ряду, одержаного в результаті почленного диференціювання даного ряду відповідне число разів; при цьому інтервал збіжності кожного ряду, одержаного в результаті диференціювання, є той же інтервал

Приклад 1. Знайти інтервали збіжності степеневих рядів.

а) 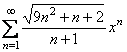; б) .

Р о з в ‘ я з о к. а) Знайдемо радіус збіжності степеневого ряду за формулою (13.44)

.

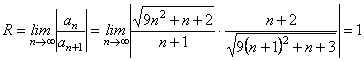Дослідимо збіжність ряду на кінцях інтервалу, тобто при

При : 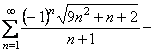розбігається, тому що

При : 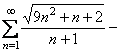розбігається (не виконується

необхідна умова збіжності). Отже, ряд збігається при

б) За формулою (13.45) знаходимо радіус збіжності

При : .

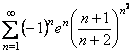Оскільки

, то

знакочергуючий ряд розбігається.

При : 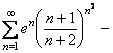розбігається (не виконується

необхідна ознака збіжності. Інтервал збіжності даного ряду

Приклад 2. Знайти суму ряду

Р о з в ‘ я з о к. Позначимо суму цього степеневого ряду через Радіус збіжності даного ряду а інтервал збіжності Продиференціюємо почленно його два рази (наслідок теореми 2) :

Останній ряд рівномірно збігається всередині проміжку і представляє собою суму нескінченно спадної геометричної прогресії із знаменником а тому сума

Зауважимо, що

Розв’язуючи дане диференціальне рівняння із заданими початковими умовами, одержимо:

Оскільки то і сума заданого ряду